
���Ű����������ֺ�֮����ָ�Ӳ���������һ��������������Ⱥ����ʱ��ס������Ϊ�����壬��2.5�ף�ǰ��ǽ��2.5�ߵIJ�ɫ�ְ壬������2.5�ߵĸ��ϸְ壬���ְָ�ļ۸��ó��������㣨���ְ�ĸ߾�Ϊ2.5�ף��ó��ȳ��Ե��۾������ְ�ļ۸�ÿ���ۣ���ɫ�ְ�Ϊ450Ԫ�����ϸְ�Ϊ200Ԫ���������������Ͻ��죬ÿƽ���ײ��Ϸ�Ϊ200Ԫ��ÿ�����Ϸѿ�����32000Ԫ���ڡ�
��1���跿ǰ��ǽ�ij�Ϊ ������ǽ�ij�Ϊ
������ǽ�ij�Ϊ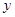 ��һ�������ò��Ϸ�Ϊp������
��һ�������ò��Ϸ�Ϊp������ ��
��
��2��һ�������S�����ֵ�Ƕ��٣���S���ʱ��ǰ��ǽ�ij����Ƕ��٣�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪x��0��y��0����x+8y��xy=0����
����xy����Сֵ��
����x+y����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij��ֽ���⽨һ��ƽ��ͼ��Ϊ���������Ϊ162m2��������ˮ�����أ��ص����һ��(ƽ��ͼ��ͼ��ʾ)�����������Χǽ���쵥��Ϊ400Ԫ/m2���м�������ǽ���쵥��Ϊ248Ԫ/m2���ص��쵥��Ϊ80Ԫ/m2��ˮ������ǽ�ĺ�Ⱥ��Բ��ƣ�
(1)�������ˮ�����صij��Ϳ���ʹ�������ͣ�������������ۣ�
(2)�����ڵ������ƣ��óصij��Ϳ������ܳ���16m���������ˮ�صij��Ϳ���ʹ�������ͣ�������������ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�۲������������ۣ�
������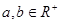 ����
����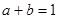 ����
����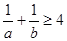 ��
��
������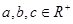 ����
����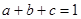 ����
����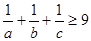 ��
��
��֤�����ۣ�������ȣ������ۣ�����д��һ������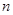 ������
������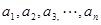 �Ľ��ۣ���д�����ۣ�����֤����
�Ľ��ۣ���д�����ۣ�����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ���ѡ��
��֪����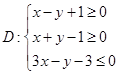 �����Ϊ
�����Ϊ ���㼯
���㼯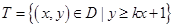 ������ϵ�ж�Ӧ��������Ϊ
������ϵ�ж�Ӧ��������Ϊ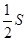 ����
���� ��ֵΪ�� ��
��ֵΪ�� ��
A�� | B�� | C�� | D�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com