
(9分)设x>0,y>0且x+y=1,求证: ≥9.
≥9.
科目:高中数学 来源: 题型:解答题
已知函数 的定义域为
的定义域为 . 设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
. 设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
(1)求证: 是定值;
是定值;
(2)判断并说明 有最大值还是最小值,并求出此最大值或最小值.
有最大值还是最小值,并求出此最大值或最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在雅安发生地震灾害之后,救灾指挥部决定建造一批简易房,供灾区群众临时居住,房形为长方体,高2.5米,前后墙用2.5米高的彩色钢板,两侧用2.5米高的复合钢板,两种钢板的价格都用长度来计算(即钢板的高均为2.5米,用长度乘以单价就是这块钢板的价格),每米单价:彩色钢板为450元,复合钢板为200元,房顶用其他材料建造,每平方米材料费为200元,每套房材料费控制在32000元以内。
(1)设房前面墙的长为 ,两侧墙的长为
,两侧墙的长为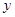 ,一套简易房所用材料费为p,试用
,一套简易房所用材料费为p,试用 。
。
(2)一套简易房面积S的最大值是多少?当S最大时,前面墙的长度是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知正方形ABCD,其中顶点A、C坐标分别是 (2,0)、(2,4),点P(x,y)在正方形内部(包括边界)上运动,则 的最大值是
的最大值是
A.10 B.8 C.12 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com