
已知 ,证明:
,证明: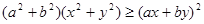 ,并利用上述结论求
,并利用上述结论求 的最小值(其中
的最小值(其中 .
.
见解析;
解析试题分析:可用作差比较;作差比较大小的关键是恰当变形,达到易于判断符号的目的,而常用的变形方法有配方法、因式分解等如本题中将 作差后关键就是变形确定符号,将其展开 后合并同类项得
作差后关键就是变形确定符号,将其展开 后合并同类项得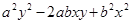 ,这个式子刚好就是一个完全平方
,这个式子刚好就是一个完全平方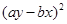 ,而
,而 ,所以有
,所以有 。也可以用分析法等来证明。分析法是从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为判定这些充分条件是否具备的问题。如果能够肯定这些充分条件都已具备,那么就可以断定原不等式成立,这种证明方法叫做分析法。如本题中要证明
。也可以用分析法等来证明。分析法是从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为判定这些充分条件是否具备的问题。如果能够肯定这些充分条件都已具备,那么就可以断定原不等式成立,这种证明方法叫做分析法。如本题中要证明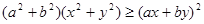 ,则找使得这个不等式成立的充分条件
,则找使得这个不等式成立的充分条件 依次找下去,最后得到
依次找下去,最后得到 (显然成立),所以不等式得证。
(显然成立),所以不等式得证。
试题解析: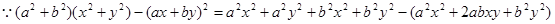
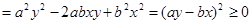 4分
4分 7分
7分
(法二)要证明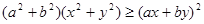
只要证 2分
2分
即证 4分
4分
即证 (显然成立)
(显然成立)
故原不等式得证 7分
由不等式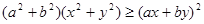 成立
成立
知 , 10分
, 10分
即最小值为25,当且仅当 时等号成立。 13分
时等号成立。 13分
考点:不等式的证明及基本不等式的应用。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
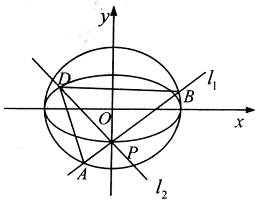
如图,点 是椭圆
是椭圆 的一个顶点,
的一个顶点, 的长轴是圆
的长轴是圆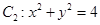 的直径,
的直径,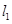 、
、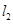 是过点
是过点 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中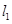 交圆
交圆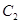 于
于 、
、 两点,
两点,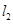 交椭圆
交椭圆 于另一点
于另一点 .
.
(1)求椭圆 的方程;
的方程;
(2)求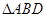 面积的最大值及取得最大值时直线
面积的最大值及取得最大值时直线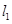 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com