
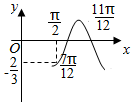
 已知函数f(x)=Acos(ωx+φ)的图象如图所示,则f($\frac{5π}{6}$)=( )
已知函数f(x)=Acos(ωx+φ)的图象如图所示,则f($\frac{5π}{6}$)=( )| A. | -$\frac{2}{3}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 根据图象便可求出函数f(x)的半个周期为$\frac{π}{3}$,从而可得出一个周期的大小,进而便可求出ω=3,这样f(x)=Acos(3x+φ),而由图象看出$f(\frac{π}{2})=-\frac{2}{3}$,从而得出$Asinφ=-\frac{2}{3}$,而可求得$f(\frac{5π}{6})=-Asinφ$,从而便可得出$f(\frac{5π}{6})$的值.
解答 解:根据图象看出函数f(x)的半个周期为$\frac{11π}{12}-\frac{7π}{12}=\frac{π}{3}$;
∴f(x)的周期为$\frac{2π}{ω}=\frac{2π}{3}$;
∴ω=3;
∴f(x)=Acos(3x+φ);
由图象看出$Acos(\frac{3π}{2}+φ)=Asinφ=-\frac{2}{3}$;
∴$f(\frac{5π}{6})=Acos(\frac{5π}{2}+φ)=Acos(\frac{π}{2}+φ)$=$-Asinφ=\frac{2}{3}$.
故选:D.
点评 考查函数f(x)=Acos(ωx+φ)的图象特点,以及该函数周期的计算公式,清楚函数f(x)=Acos(ωx+φ)是如何由f(x)=cosx变换来的,以及三角函数的诱导公式,已知函数求值的方法.


科目:高中数学 来源: 题型:填空题
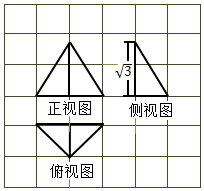 网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为$\frac{16π}{3}$.
网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为$\frac{16π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{3}$,$\sqrt{3}$) | B. | (-1,1) | C. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 15 | C. | 32 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α=1 | B. | 0<α<1 | C. | 2<α<3 | D. | 1<α<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x<2} | B. | {x|-2<x<2} | C. | {0,1} | D. | {-2,0,1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com