
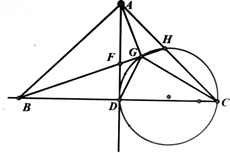
 已知CD是圆上的一条弦,延长CD与B点使得CD=BD,过D作BC的中垂线在中垂线上找到一点A使得AB⊥AC,连接AC交圆与H点连接BH,分别交AD与F点,交圆与G点,连接DG.求证:四边形ABDG有外接圆.
已知CD是圆上的一条弦,延长CD与B点使得CD=BD,过D作BC的中垂线在中垂线上找到一点A使得AB⊥AC,连接AC交圆与H点连接BH,分别交AD与F点,交圆与G点,连接DG.求证:四边形ABDG有外接圆. 分析 先由割线定理得BD•BC=BG•BH,再由图中的等量关系,得BD•BC=2BD2=AB2=BG•BH,证明△BAH∽△BGA,从而得出∠AGB=∠HAB=90°,即AG⊥GB,再由DB⊥AD,即可得证.
解答 证明:如图所示,由割线定理,得BD•BC=BG•BH,
∵CD=BD=AD,DA⊥BC,
∴AC=AB=$\sqrt{2}$BD,∠BAD=∠CAD=45°,
∴△CBA是等腰直角三角形,即∠CAB=90°,
∴BD•BC=2BD2=AB2=BG•BH,即$\frac{AB}{BG}$=$\frac{BH}{AB}$,
又∵∠ABG=∠ABH,∴△BAH∽△BGA,
∴∠AGB=∠HAB=90°,即AG⊥GB.
又DB⊥AD,
可得四边形ABDG有外接圆.
点评 本题主要考查圆中的垂直关系、割线定理、三角形相似等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
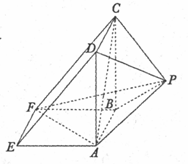 如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.
如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
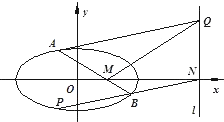 过点M(1,0)的直线交椭圆$\frac{{x}^{2}}{4}$+y2=1于A、B两点,直线l:x=4与x轴交于点N,设点A关于x轴的对称点为P(异于点B).
过点M(1,0)的直线交椭圆$\frac{{x}^{2}}{4}$+y2=1于A、B两点,直线l:x=4与x轴交于点N,设点A关于x轴的对称点为P(异于点B).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①和④ | B. | ②和④ | C. | ②和⑤ | D. | ③和⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在等边△ABC中,点D,E分别在边AC,AB上,且AD:DC=1:2,AE:AB=2:3,BD与CE相交于点F.
如图,在等边△ABC中,点D,E分别在边AC,AB上,且AD:DC=1:2,AE:AB=2:3,BD与CE相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com