
| A. | ①和④ | B. | ②和④ | C. | ②和⑤ | D. | ③和⑤ |
分析 求函数的定义域和函数的导数,研究函数单调性和极值,利用极值、最值的关系确定f(x0)的值,进行判断即可.
解答 解:函数的定义域为(0,+∞),f(x)=(-$\frac{x}{x+1}$)lnx,
函数的导数f′(x)=(-$\frac{x}{x+1}$)′lnx-$\frac{x}{x+1}$•$\frac{1}{x}$=$\frac{-lnx-x-1}{(x+1)^{2}}$,
设h(x)=-lnx-x-1,
则h′(x)=$\frac{-1-x}{x}$,则当x>0时,h′(x)<0,即h(x)在(0,+∞)上为减函数,
∵h(1)<-1-1=-2<0,当x→0时,h(x)>0,
∴在(0,1)内函数h(x)有唯一的零点x0,即h(x0)=-lnx0-x0-1=0,
即lnx0=-1-x0,
当0<x<x0,f′(x)>0,当x>x0,f′(x)<0,即函数f(x)在x=x0处取得最大值,
即f(x0)=(-$\frac{{x}_{0}}{{x}_{0}+1}$)•lnx0=(-$\frac{{x}_{0}}{{x}_{0}+1}$)•(-1-x0)=x0,②正确;
∵h($\frac{1}{2}$)=-ln$\frac{1}{2}$-$\frac{1}{2}-1$=ln2-$\frac{3}{2}$<0,
∴0<x0<$\frac{1}{2}$,∴$f({x_0})<\frac{1}{2}$,
故选:B.
点评 本题主要考查命题的真假判断涉及函数的单调性,极值,最值与导数之间的关系,综合性较强,运算量较大.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
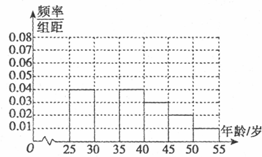 近几年骑车锻炼越来越受到人们的喜爱,男女老少踊跃参加,我校课外活动小组利用春节放假时间进行社会实践,将被调查人员分为“喜欢骑车”和“不喜欢骑车”,得到如表统计表和各年龄段人数频率分布直方图:
近几年骑车锻炼越来越受到人们的喜爱,男女老少踊跃参加,我校课外活动小组利用春节放假时间进行社会实践,将被调查人员分为“喜欢骑车”和“不喜欢骑车”,得到如表统计表和各年龄段人数频率分布直方图:| 组数 | 分组 | 喜欢骑车锻炼的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
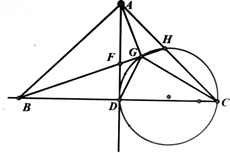 已知CD是圆上的一条弦,延长CD与B点使得CD=BD,过D作BC的中垂线在中垂线上找到一点A使得AB⊥AC,连接AC交圆与H点连接BH,分别交AD与F点,交圆与G点,连接DG.求证:四边形ABDG有外接圆.
已知CD是圆上的一条弦,延长CD与B点使得CD=BD,过D作BC的中垂线在中垂线上找到一点A使得AB⊥AC,连接AC交圆与H点连接BH,分别交AD与F点,交圆与G点,连接DG.求证:四边形ABDG有外接圆.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com