
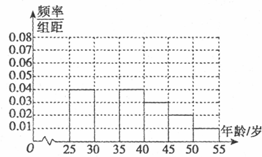
 �������ﳵ����Խ��Խ�ܵ����ǵ�ϲ������Ů����ӻԾ�μӣ���У����С�����ô��ڷż�ʱ��������ʵ��������������Ա��Ϊ��ϲ���ﳵ���͡���ϲ���ﳵ�����õ����ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
�������ﳵ����Խ��Խ�ܵ����ǵ�ϲ������Ů����ӻԾ�μӣ���У����С�����ô��ڷż�ʱ��������ʵ��������������Ա��Ϊ��ϲ���ﳵ���͡���ϲ���ﳵ�����õ����ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��| ���� | ���� | ϲ���ﳵ���������� | ռ�����Ƶ�� |
| ��һ�� | [25��30�� | 120 | 0.6 |
| �ڶ��� | [30��35�� | 195 | p |
| ������ | [35��40�� | 100 | 0.5 |
| ������ | [40��45�� | a | 0.4 |
| ������ | [45��50�� | 30 | 0.3 |
| ������ | [50��55] | 15 | 0.3 |
���� ��1������Ƶ��ֱ��ͼ�����ʣ�����Ƶ�ʺ�Ϊ1��Ƶ�ʵļ��㹫ʽ���ɵó���
��2����[40��45������εġ�ϲ���ﳵ����[45��50������εġ�ϲ���ﳵ���ı�ֵΪ60��30=2��1���ɵò��÷ֲ��������ȡ18�ˣ�[40��45������12�ˣ�[45��50������6�ˣ������������X���ӳ����ηֲ����ɵó���
��� �⣺��1���ڶ����Ƶ��Ϊ1-��0.04+0.04+0.03+0.02+0.01����5=0.3��
���Ϊ$\frac{0.3}{5}=0.06$��Ƶ��ֱ��ͼ���£�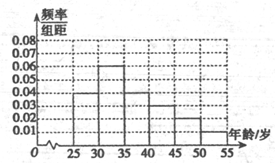
��һ�������Ϊ$\frac{120}{0.6}=200$��Ƶ��Ϊ0.04��5=0.2��
��$n=\frac{200}{0.2}=1000$��
�����֪���ڶ����Ƶ��Ϊ0.06��5=0.3��
��ڶ��������Ϊ1000��0.3=300����$p=\frac{195}{300}=0.65$��
�������Ƶ��Ϊ0.03��5=0.15��
������������Ϊ1000��0.15=150����a=150��0.4=60��
��2����[40��45������εġ�ϲ���ﳵ����[45��50������εġ�ϲ���ﳵ���ı�ֵΪ60��30=2��1��
����÷ֲ��������ȡ18�ˣ�[40��45������12�ˣ�[45��50������6�ˣ�
���������X���ӳ����ηֲ���
��$P��X=0��=\frac{{C_{12}^0C_6^3}}{{C_{18}^3}}=\frac{5}{204}$��$P��X=1��=\frac{{C_{12}^1C_6^2}}{{C_{18}^3}}=\frac{15}{68}$��$P��X=2��=\frac{{C_{12}^2C_6^1}}{{C_{18}^3}}=\frac{33}{68}$��$P��X=3��=\frac{{C_{12}^3C_6^0}}{{C_{18}^3}}=\frac{55}{204}$��
���������X�ķֲ���Ϊ��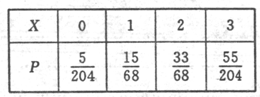
��$EX=0��\frac{5}{204}+1��\frac{15}{68}+2��\frac{33}{68}+3��\frac{55}{204}=2$��
���� ���⿼����Ƶ��ֱ��ͼ�����ʡ������ηֲ������ʣ�������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1��2��3} | B�� | {x|1��x��3} | C�� | {2��3} | D�� | {x|1��x��$\sqrt{10}$} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 2 | C�� | $\sqrt{2}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -2 | C�� | -3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
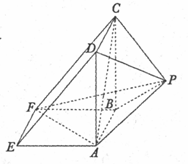 ��ͼ��ʾ���ü���������һ��ֱ������ADE-BCF��һ��������P-ABCD��϶��ɣ�AD��AF��AE=AD=2��
��ͼ��ʾ���ü���������һ��ֱ������ADE-BCF��һ��������P-ABCD��϶��ɣ�AD��AF��AE=AD=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ٺ͢� | B�� | �ں͢� | C�� | �ں͢� | D�� | �ۺ͢� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com