
分析 (1)对x讨论,分当x<-1时,当-1≤x≤$\frac{1}{2}$时,当x>$\frac{1}{2}$时,去掉绝对值,解不等式,最后求并集即可;
(2)由题意可得|2x-1|+|x+1|>a恒成立,令g(x)=|2x-1|+|x+1|,对x讨论,分当x<-1时,当-1≤x≤$\frac{1}{2}$时,当x>$\frac{1}{2}$时,去掉绝对值,运用单调性可得最小值,即可得到a的范围.
解答 解:(1)当x<-1时,1-2x-(-x-1)≤0,即x≥2,可得x∈∅;
当-1≤x≤$\frac{1}{2}$时,1-2x-(x+1)≤0,即x≥0,可得0≤x≤$\frac{1}{2}$;
当x>$\frac{1}{2}$时,2x-1-(x+1)≤0,即x≤2,可得$\frac{1}{2}$<x≤2.
综上可得,原不等式的解集为[0,2];
(2)f(x)>a-2|x+1|恒成立,即为|2x-1|+|x+1|>a恒成立,
令g(x)=|2x-1|+|x+1|,
当x<-1时,g(x)=1-2x+(-x-1)=-3x,可得g(x)>3;
当-1≤x≤$\frac{1}{2}$时,g(x)=1-2x+(x+1)=2-x,可得g(x)∈[$\frac{3}{2}$,3];
当x>$\frac{1}{2}$时,g(x)=2x-1+(x+1)=3x,可得g(x)>$\frac{3}{2}$.
则g(x)的最小值为$\frac{3}{2}$.
即有a<$\frac{3}{2}$,
则实数a的取值范围是(-∞,$\frac{3}{2}$).
点评 本题考查绝对值不等式的解法,注意运用分类讨论的思想方法,考查不等式恒成立问题的解法,注意运用参数分离和函数的单调性,属于中档题.


科目:高中数学 来源: 题型:解答题
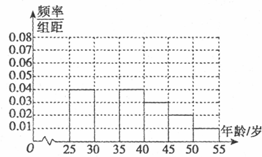 近几年骑车锻炼越来越受到人们的喜爱,男女老少踊跃参加,我校课外活动小组利用春节放假时间进行社会实践,将被调查人员分为“喜欢骑车”和“不喜欢骑车”,得到如表统计表和各年龄段人数频率分布直方图:
近几年骑车锻炼越来越受到人们的喜爱,男女老少踊跃参加,我校课外活动小组利用春节放假时间进行社会实践,将被调查人员分为“喜欢骑车”和“不喜欢骑车”,得到如表统计表和各年龄段人数频率分布直方图:| 组数 | 分组 | 喜欢骑车锻炼的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
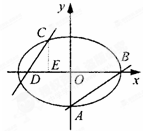 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$(a>b>0)的离心率$e=\frac{{\sqrt{6}}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{{\sqrt{3}}}{2}$.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$(a>b>0)的离心率$e=\frac{{\sqrt{6}}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com