Question

1．如图，P为△ABC内一点，使得∠PAB=10°，∠PBA=20°，∠PCA=30°，∠PAC=40°．求证：△ABC是等腰三角形．

Answer 1

分析 由∠PCB=30°联想到等边三角形，将△BPC沿着PC翻折到△DPC的位置，连接DB、DP、DA，易证△DCB是等边三角形，由此可得到∠PDB=∠PBD=20°=∠BAP，从而可得A、P、B、D四点共圆，根据圆周角定理可得∠ADP=∠ABP=10°，由此可得到∠ADB=30°=∠ADC，从而可证到△ADB≌△ADC，则有AB=AC．

解答 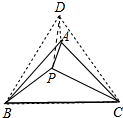证明：将△BPC沿着PC翻折到△DPC的位置，连接DB、DP、DA，如图，
根据轴对称的性质可得：PD=PB，CD=CB，∠DCP=∠BCP=30°，
∴∠DCB=60°，
∴△DCB是等边三角形，
∴∠DBC=∠BDC=60°，DB=DC，
∴∠PDB=∠PBD=∠DBC-∠PBC=60°-40°=20°，
∵∠BAP=20°，∴∠PDB=∠BAP，
∴A、P、B、D四点共圆，
∴∠ADP=∠ABP=10°，
∴∠ADB=∠PDB+∠ADP=20°+10°=30°，
∴∠ADC=∠BDC-∠ADB=60°-30°=30°，
∴∠ADB=∠ADC．
∴△ADB≌△ADC，
∴AB=AC，
∴△ABC是等腰三角形．

点评 本题主要考查了等边三角形的判定与性质、全等三角形的判定与性质、四点共圆的判定、圆周角定理、等腰三角形的性质、轴对称的性质等知识，有一定的难度，由30°角联想到等边三角形是解决本题的关键．