
分析 (1)求导数,可得切线的斜率,即可求函数f(x)在点(1,0)处的切线方程;
(2)由g(x)-2f(x)≤0,有a≤2lnx+x+$\frac{3}{x}$,求出右边的最小值,即可求实数a的取值范围;
(3)问题等价于xlnx>$\frac{x}{{e}^{x}}$-$\frac{2}{e}$,由(1)知,f(x)的最小值是-$\frac{1}{e}$,右边取得最大值-$\frac{1}{e}$,即可证明结论.
解答 (1)解:∵f(x)=xlnx,
∴f′(x)=lnx+1,
∴f′(1)=1,
∴函数f(x)在点(1,0)处的切线方程为y=x-1;
(2)解:由g(x)-2f(x)≤0,有a≤2lnx+x+$\frac{3}{x}$,
设h(x)=2lnx+x+$\frac{3}{x}$(x>0),则h′(x)=$\frac{(x+3)(x-1)}{{x}^{2}}$,
①x∈(0,1),h'(x)<0,h(x)单调递减,②x∈(1,+∞),h'(x)>0,h(x)单调递增,
所以h(x)min=h(1)=4,
对一切x∈(0,+∞),g(x)-2f(x)≤0恒成立,所以a≤h(x)min=4;
(3)证明:问题等价于xlnx>$\frac{x}{{e}^{x}}$-$\frac{2}{e}$,
由(1)知,f(x)的最小值是-$\frac{1}{e}$,当且仅当x=$\frac{1}{e}$时取等号,
设y=$\frac{x}{{e}^{x}}$-$\frac{2}{e}$,则y′=$\frac{1-x}{{e}^{x}}$,
∴0<x<1,y′>0,x>1,y′<0,
∴函数在(0,1]上为增函数,在[1,+∞)上为减函数,
∴x=1时ymax=-$\frac{1}{e}$,
∴exlnx+$\frac{2{e}^{x-1}}{x}$>1.
点评 本题考查导数的几何运用,考查恒成立问题,考查不等式的证明,正确分离参数是关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
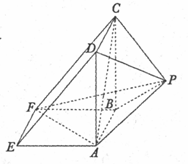 如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.
如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①和④ | B. | ②和④ | C. | ②和⑤ | D. | ③和⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在等边△ABC中,点D,E分别在边AC,AB上,且AD:DC=1:2,AE:AB=2:3,BD与CE相交于点F.
如图,在等边△ABC中,点D,E分别在边AC,AB上,且AD:DC=1:2,AE:AB=2:3,BD与CE相交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com