
分析 由已知中函数y=log${\;}_{\frac{1}{2}}$(x2+x-2)的解析式,先确定函数的定义域,进而根据二次函数和对数函数的性质,分别判断内,外函数的单调性,进而根据复合函数“同增异减”的原则,得到答案.
解答 解:由题意,x2+x-2>0,∴x<-2或x>1,
函数y=log${\;}_{\frac{1}{2}}$(x2+x-2)的定义域为(-∞,-2)∪(1,+∞)
令t=x2+x-2,则y=log${\;}_{\frac{1}{2}}$t
∵y=log${\;}_{\frac{1}{2}}$t为减函数
t=x2+x-2的单调递减区间是(-∞,-$\frac{1}{2}$),单调递增区间是(-$\frac{1}{2}$,+∞)
故函数y=log${\;}_{\frac{1}{2}}$(x2+x-2)的单调递增区间是(-∞,-2).
点评 本题考查的知识点是二次函数的图象和性质,对数函数的单调区间,复合函数的单调性,其中复合函数单调性“同增异减”的原则,是解答本题的关键.


科目:高中数学 来源: 题型:解答题
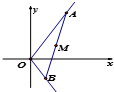 如图,点A,B分别在射线l1:y=2x(x≥0),l2:y=-2x(x≥0)上运动,且S△AOB=4.
如图,点A,B分别在射线l1:y=2x(x≥0),l2:y=-2x(x≥0)上运动,且S△AOB=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
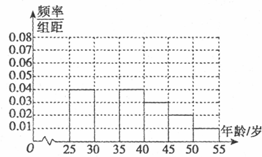 近几年骑车锻炼越来越受到人们的喜爱,男女老少踊跃参加,我校课外活动小组利用春节放假时间进行社会实践,将被调查人员分为“喜欢骑车”和“不喜欢骑车”,得到如表统计表和各年龄段人数频率分布直方图:
近几年骑车锻炼越来越受到人们的喜爱,男女老少踊跃参加,我校课外活动小组利用春节放假时间进行社会实践,将被调查人员分为“喜欢骑车”和“不喜欢骑车”,得到如表统计表和各年龄段人数频率分布直方图:| 组数 | 分组 | 喜欢骑车锻炼的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com