
分析 (1)由条件得$\frac{1}{a^2}+\frac{1}{b^2}=1$,且c2=2b2,a2=3b2,解出即可得出.
(2)解法1:若直线l1斜率为0,则直线l2斜率不存在,可得所求直线MN的方程为x+y=0;同理可得,当直线l2斜率为0,直线l1斜率不存在时,所求直线MN的方程为x+y=0.若直线l1斜率存在且不为0,设l1方程为y+1=k(x+1),与椭圆方程联立可得:(1+3k2)x2+6k(k-1)x+3(k-1)2-4=0.解得M,N坐标,根据线段MN中点在x轴上,解得k即可得出.
解法2:设M(x1,y1),N(x2,y2),则${x_1}^2+3{y_1}^2=4,{x_2}^2+3{y_2}^2=4$,两式相减得根据线段MN的中点在x轴上,可得(x1+x2)(x1-x2)=0. 分类讨论,利用相互垂直与数量积的关系即可得出.
解答 解:(1)由条件得$\frac{1}{a^2}+\frac{1}{b^2}=1$,且c2=2b2,
∴a2=3b2,解得${b^2}=\frac{4}{3}$,a2=4.
∴椭圆方程为:$\frac{x^2}{4}+\frac{{3{y^2}}}{4}=1$.
(2)解法1:若直线l1斜率为0,则直线l2斜率不存在,此时M(1,-1),N(-1,1),满足两点连线段中点在x轴上,所求直线MN的方程为x+y=0;
同理可得,当直线l2斜率为0,直线l1斜率不存在时,所求直线MN的方程为x+y=0.
若直线l1斜率存在且不为0,设l1方程为y+1=k(x+1),
联立$\left\{\begin{array}{l}y=kx+k-1\\{x^2}+3{y^2}=4\end{array}\right.$,消去y得(1+3k2)x2+6k(k-1)x+3(k-1)2-4=0.
∵P为(-1,-1),解得$M(\frac{{-3{k^2}+6k+1}}{{1+3{k^2}}},\frac{{3{k^2}+2k-1}}{{1+3{k^2}}})$,
用$-\frac{1}{k}$代替k,得$N(\frac{{{k^2}-6k-3}}{{{k^2}+3}},\frac{{-{k^2}-2k+3}}{{{k^2}+3}})$.
∵线段MN中点在x轴上,则$\frac{{3{k^2}+2k-1}}{{1+3{k^2}}}+\frac{{-{k^2}-2k+3}}{{{k^2}+3}}=0$,
整理得:k3-4k2-k=0,∵k≠0,解得$k=2±\sqrt{5}$.
此时$M({-\frac{1}{2},\frac{{\sqrt{5}}}{2}}),N({-\frac{1}{2},-\frac{{\sqrt{5}}}{2}})$,或者$M({-\frac{1}{2},-\frac{{\sqrt{5}}}{2}}),N({-\frac{1}{2},\frac{{\sqrt{5}}}{2}})$.
所求直线MN的方程为$x=-\frac{1}{2}$.
综上可得,所求直线MN的方程为x+y=0或者$x=-\frac{1}{2}$.
解法2:设M(x1,y1),N(x2,y2),则${x_1}^2+3{y_1}^2=4,{x_2}^2+3{y_2}^2=4$,
两式相减得(x1+x2)(x1-x2)+3(y1+y2)(y1-y2)=0.
∵线段MN的中点在x轴上,∴y1+y2=0,从而可得(x1+x2)(x1-x2)=0.
若x1+x2=0,则N(-x1,-y1).
∵PM⊥PN,∴$\overrightarrow{PM}•\overrightarrow{PN}=0$,得${x_1}^2+{y_1}^2=2$.
又∵${x_1}^2+3{y_1}^2=4$,∴解得x1=±1,
∴M(-1,1),N(1,-1)或M(1,-1),N(-1,1).
∴直线MN的方程为y=-x.
若x1-x2=0,则N(x1,-y1),
∵PM⊥PN,∴$\overrightarrow{PM}•\overrightarrow{PN}=0$,得${y_1}^2={({x_1}+1)^2}+1$.
又∵${x_1}^2+3{y_1}^2=4$,∴解得${x_1}=-\frac{1}{2}$或-1,
经检验:${x_1}=-\frac{1}{2}$满足条件,x1=-1不满足条件.
综上,直线MN的方程为x+y=0或$x=-\frac{1}{2}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为一元二次方程的根与系数的关系、向量垂直与数列解得关系、中点坐标公式,考查了分类讨论方法、推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
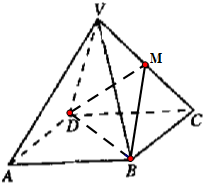 如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为$\sqrt{5}$的等腰三角形,M为VC边中点.
如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为$\sqrt{5}$的等腰三角形,M为VC边中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3} | B. | {x|1<x<3} | C. | {2,3} | D. | {x|1<x<$\sqrt{10}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | -3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
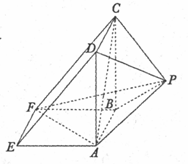 如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.
如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
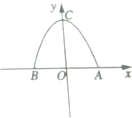 如图,抛物线y=-x2+4交x轴于A,B两点,顶点为C
如图,抛物线y=-x2+4交x轴于A,B两点,顶点为C查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①和④ | B. | ②和④ | C. | ②和⑤ | D. | ③和⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com