
分析 (Ⅰ)由题定义域为{x|x<0},由在x=-1时取极值,可得f′(-1)=0,解得a并验证即可得出.
(Ⅱ)g(x)=f(-x)+2x=lnx+$\frac{1}{x}$+2x(x>0),g′(x)=$\frac{(2x-1)(x+1)}{{x}^{2}}$,利用导数研究单调性极值与最值即可得出.
解答 解:(Ⅰ)由题定义域为{x|x<0},
f′(x)=$\frac{1}{x}+a+\frac{1}{{x}^{2}}$=$\frac{a{x}^{2}+x+1}{{x}^{2}}$,
∵在x=-1时取极值,∴f′(-1)=$\frac{a}{{x}^{2}}$=0,解得a=0.
经过验证a=0满足条件.
(Ⅱ)g(x)=f(-x)+2x=lnx+$\frac{1}{x}$+2x(x>0),
g′(x)=$\frac{1}{x}-\frac{1}{{x}^{2}}$+2=$\frac{2{x}^{2}+x-1}{{x}^{2}}$=$\frac{(2x-1)(x+1)}{{x}^{2}}$,
∴g(x)在$(0,\frac{1}{2}]$上单调递减,在$[\frac{1}{2},+∞)$上单调递增.
∴g(x)在x=$\frac{1}{2}$取得最小值$g(\frac{1}{2})$=3-ln2.
点评 本题考查了利用导数研究单调性极值与最值,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
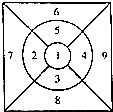 如图,图案共分9个区域,有6种不同颜色的涂料可供涂色,每个区域只能涂一种颜色的涂料,其中2和9同色、3和6同色、4和7同色、5和8同色,且相邻区域的颜色不相同,则涂色方法有( )
如图,图案共分9个区域,有6种不同颜色的涂料可供涂色,每个区域只能涂一种颜色的涂料,其中2和9同色、3和6同色、4和7同色、5和8同色,且相邻区域的颜色不相同,则涂色方法有( )| A. | 360种 | B. | 720种 | C. | 780种 | D. | 840种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com