
分析 (1)利用诱导公式化简求解函数的解析式即可.
(2)求出正切函数值,然后利用同角三角函数基本关系式求解即可.
解答 解:(1)f(α)=$\frac{sin(-α-π)cos(5π-α)tan(4π-α)}{cos(\frac{5π}{2}-α)tan(-α-π)}$=$\frac{sinαcosαtanα}{-sinαtanα}$=-cosα.
(2)tan(α-π)=-3,可得tanα=-3.$\left\{\begin{array}{l}{\frac{sinα}{cosα}=-3}\\{si{n}^{2}α+co{s}^{2}α=1}\end{array}\right.$,
可得cos2$α=\frac{1}{10}$,
α是第四象限角,
∴cosα=$\frac{\sqrt{10}}{10}$.
f(α)=-$\frac{\sqrt{10}}{10}$.
点评 本题考查诱导公式的应用,同角三角函数基本关系式的应用,考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
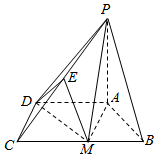 已知四棱锥P-ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形,$PA=DM=2\sqrt{3}$.
已知四棱锥P-ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形,$PA=DM=2\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.1588 | B. | 0.1587 | C. | 0.1586 | D. | 0.1585 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 332 | B. | -332 | C. | 320 | D. | -320 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com