
| A. | 1 | B. | $\frac{4}{e^2}$ | C. | $\frac{1}{2}$ | D. | $\frac{8}{e^2}$ |
分析 求出切点Q的坐标,再求出函数的导数,并求出切线的斜率k,设出R点的坐标,由两点的斜率公式,写出斜率k,并求出r,求出△PQRS的面积为S,再运用导数求出S的最大值即可.
解答 解:∵PQ∥y轴,P(a,0),
∴Q(a,f(a))即(a,2lna),
又f(x)=ln(ax)(0<a<1)的导数f′(x)=$\frac{1}{x}$,
∴过Q的切线斜率k=$\frac{1}{a}$,
设R(r,0),
则k=$\frac{2lna}{a-r}$=$\frac{1}{a}$,
∴r=a-2alna,
即R(a-2alna,0),PR=2alna,
∴△PQR的面积为S=2a(lna)2,
导数S′=2lna(lna+2),由S′=0得a=e-2,
当1>a>e-2时,S′<0,当0<a<e-2时,S′>0,
∴a=e-2为极大值点,也为最大值点,
∴△PQR的面积的最大值为$\frac{8}{{e}^{2}}$.
故选D.
点评 本题主要考查导数的概念和应用,考查应用导数求切线方程,同时考查运用导数求最值,考查基本的运算能力,是一道中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | $y=±\frac{1}{3}x$ | C. | $y=±\sqrt{3}x$ | D. | $y=±\frac{{\sqrt{3}}}{3}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{10}{3}$ | C. | 6 | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
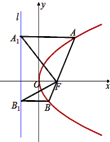 如图,过抛物线C:y2=2px(p>0)的焦点F作直线交C于A、B两点,过A、B分别向C的准线l作垂线,垂足为A1、B1,已知△AA1F与△BB1F的面积分别为9和1,则△A1B1F的面积为( )
如图,过抛物线C:y2=2px(p>0)的焦点F作直线交C于A、B两点,过A、B分别向C的准线l作垂线,垂足为A1、B1,已知△AA1F与△BB1F的面积分别为9和1,则△A1B1F的面积为( )| A. | 4 | B. | 6 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com