
分析 由数列的递推式:当n=1时,b1=T1;当n≥2时,bn=Tn-Tn-1,求得bn,an,λan-bn≥8(n-3)+2λ等价于(λ-3)•2n-1≥8(n-3),运用参数分离和数列的单调性,可得最值,解不等式即可得到所求范围.
解答 解:依题设,当n=1时,b1=T1=3;
当n≥2时,bn=Tn-Tn-1=3(2n-1)-3(2n-1-1)=3•2n-1,
又∵当n=1时,b1=3,上式成立.
∴bn=3•2n-1.∴an=$\frac{1}{3}$bn+2=2n-1+2.
∴λan-bn≥8(n-3)+2λ等价于λ(2n-1+2)-3•2n-1≥8(n-3)+2λ,
即(λ-3)•2n-1≥8(n-3),
∴$\frac{λ-3}{16}$≥$\frac{n-3}{{2}^{n}}$对一切n∈N*恒成立,
令f(n)=$\frac{n-3}{{2}^{n}}$,则f(n+1)-f(n)=$\frac{n-2}{{2}^{n+1}}$-$\frac{n-3}{{2}^{n}}$=$\frac{4-n}{{2}^{n+1}}$,
∴当n≤4时,f(n+1)≥f(n),
当n≥5时,f(n+1)<f(n),∴当n=4或5时,f(n)取得最大值,
∴f(n)max=f(4)=f(5)=$\frac{1}{16}$,∴$\frac{λ-3}{16}$≥$\frac{1}{16}$,∴λ≥4.
故答案为:[4,+∞).
点评 本题考查数列通项公式的求法,注意运用数列递推式,考查数列不等式恒成立问题的解法,注意运用参数分离和数列的单调性,考查转化思想和运算能力,属于中档题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
 如图在正方体ABCD-A1B1C1D1中,P是上底面A1B1C1D1内一动点,PM垂直AD于M,PM=PB,则点P的轨迹为( )
如图在正方体ABCD-A1B1C1D1中,P是上底面A1B1C1D1内一动点,PM垂直AD于M,PM=PB,则点P的轨迹为( )| A. | 线段 | B. | 椭圆一部分 | C. | 抛物线一部分 | D. | 双曲线一部分 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4\sqrt{10}}{5}$ | B. | $\frac{7\sqrt{10}}{5}$ | C. | $\frac{8\sqrt{10}}{5}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
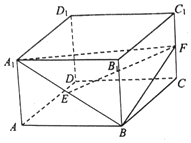 如图,在四棱柱ABCD-A1B1C1D1中,点E,F分别为A1B,C1C的中点.
如图,在四棱柱ABCD-A1B1C1D1中,点E,F分别为A1B,C1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com