练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知等腰△ABC中，AB＝BC，P在底边AC上的任一点，PE⊥AB于点E，PF⊥BC于点F，CD⊥AB于点D.求证：CD＝PE＋PF.

    【答案】见解析.

    【解析】试题分析：以的中点为原点，为轴建立平面直角坐标系，设，

    求得直线的方程，取底边上一点，求得，即可作出证明.

    试题解析：

    如图所示，以AC的中点为原点，AC为x轴建立平面直角坐标系，设A(a,0)，B(0，b)，C(－a,0)，其中a>0，b>0.

    则直线AB的方程为bx＋ay－ab＝0，

    直线BC的方程为bx－ay＋ab＝0.

    设底边AC上任意一点为P(x,0)(－a≤x≤a)，

    则|PE|＝＝，

    |PF|＝＝，

    |CD|＝＝，

    ∵|PE|＋|PF|＝＋＝＝|CD|，∴CD＝PE＋PF.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= x3﹣4x+4，
    （1）求f（x）的单调区间；
    （2）求f（x）在[0，3]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lnx，g（x）= ax+b．
    （1）若f（x）与g（x）在x=1处相切，试求g（x）的表达式；
    （2）若φ（x）= ﹣f（x）在[1，+∞）上是减函数，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x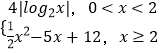）= ，若存在实数a、b、c、d，满足f（a）=f（b）=f（c）=f（d），其中d＞c＞b＞a＞0，则abcd的取值范围是（ ）
    A.（16，21）
    B.（16，24）
    C.（17，21）
    D.（18，24）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a＞0，设命题p：函数y=ax在R上单调增；命题q：不等式ax2﹣ax+1＞0对任意实数x恒成立．若p∧q假，p∨q真，则a的取值范围为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】假设关于某设备的使用年限x和所支出的维修费用y(单位:万元)有如下的统计资料:

    使用年限x/年

    2

    3

    4

    5

    6

    维修费用y/万元

    2.2

    3.8

    5.5

    6.5

    7.0

    若由资料知y对x呈线性相关关系.试求:

    (1)回归方程x+的系数.

    (2)使用年限为10年时,试估计维修费用是多少.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况，从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高，数据如下：(单位：cm)

    甲：9,10,11,12,10,20

    乙：8,14,13,10,12,21.

    (1)在给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图；

    (2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差，并由此判断甲、乙两种麦苗的长势情况．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】综合题。
    （1）四个不同球放入编号为1，2，3，4的四个盒中，则恰有一个空盒的放法有多少种？
    （2）设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的盒子现将这5个球投入5个盒子要求每个盒子放一个球，并且恰好有两个球的号码与盒子号码相同，问有多少种不同的方法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点A(m－1,2)，B(1,1)，C(3，m2－m－1)．

    (1)若A，B，C三点共线，求实数m的值；

    (2)若AB⊥BC，求实数m的值．

    查看答案和解析>>

    同步练习册答案