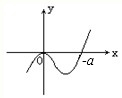
解:(1)由图可知函数的图象经过(0,0)点
∴c=0,
又图象与x轴相切于(0,0)点,f′(x)=3x
2+2ax+b
∴0=3×0
2+2a×0+b,得b=0.
∴f(x)=x
3+ax
2故方程可以继续化简为f(x)=x
3+ax
2=x
2(x+a),
令f(x)=0,可得x=0或者x=-a(a<0)
可以得到图象与x轴交点为(0,0)(-a,0)
故对-f(x)从0到-a求定积分即为所求面积,即

=
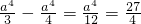
∴a=-3.(由图象知a=3舍去)
故f(x)=x
3-3x
2
(2)由(1)可知f′(x)=3x
2-6x,
设函数在点(t,f(t))处的切线方程为y=(3t
2-6t)(x-t)+(t
3-3t
2).
若切线过点(m,n),则存在实数t,使n=(3t
2-6t)(m-t)+(t
3-3t
2),
即2t
3-(3m+3)t
2+6mt+n=0.
令g(t)=2t
3-(3m+3)t
2+6mt+n,则g′(t)=6t
2-6(m+)t+6m=6(t-m)(t-1).
∵m>1
∴当t<1或t>m时,g′(t)>0;当1<t<m时,g′(t)<0.
∴g(t)在t=1时取得极大值g(1)=3m+n-1,
在t=m时取得极小值g(m)=n-f(m)
如果过点(m,n)可作函数y=f(x)的图象的三条切线,
则方程2t
3-(3m+3)t
2+6mt+n=0有三个相异的实数根,
∴
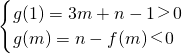
∴1-3m<n<f(m)
分析:(1)题中给出了函数的面积,故我们可以从定积分着手,求出函数以及函数与x轴的交点,建立等式求解参数,即可求出函数y=f(x)的解析式;
(2)由(1)可知f′(x)=3x
2-6x,设函数在点(t,f(t))处的切线方程为y=(3t
2-6t)(x-t)+(t
3-3t
2).若切线过点(m,n),则存在实数t,使n=(3t
2-6t)(m-t)+(t
3-3t
2),即2t
3-(3m+3)t
2+6mt+n=0.如果过点(m,n)可作函数y=f(x)的图象的三条切线,从而方程2t
3-(3m+3)t
2+6mt+n=0有三个相异的实数根,故可证1-3m<n<f(m)
点评:本题以函数为载体,考查定积分知识的运用,考查导数的几何意义,考查利用导数求函数的极值,综合性强.

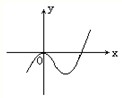 设函数f(x)=x3+ax2+bx+c的图象如图所示,且与直线y=0在原点处相切,此切线与函数图象所围区域的面积为
设函数f(x)=x3+ax2+bx+c的图象如图所示,且与直线y=0在原点处相切,此切线与函数图象所围区域的面积为 .
. 解:(1)由图可知函数的图象经过(0,0)点
解:(1)由图可知函数的图象经过(0,0)点 =
=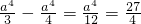
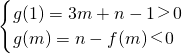


 阅读快车系列答案
阅读快车系列答案