
 某食品厂为.检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),作出样本的频率分布直方图如图所示.
某食品厂为.检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),作出样本的频率分布直方图如图所示.| C | 3 40 |
| C | 2 12 |
| C | 1 28 |
| C | 3 40 |
| C | 2 12 |
| C | 1 28 |
| 1848 |
| 9880 |
| 231 |
| 1235 |
| 231 |
| 1235 |
| ||
|
| 189 |
| 390 |
| 63 |
| 130 |
| ||||
|
| 168 |
| 390 |
| 28 |
| 65 |
| ||
|
| 33 |
| 390 |
| 11 |
| 130 |
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
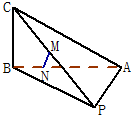 已知三棱锥P-ABC中,PA=PB,CB⊥平面PAB,PM=MC,AN=3NB.
已知三棱锥P-ABC中,PA=PB,CB⊥平面PAB,PM=MC,AN=3NB.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com