
| A. | 120° | B. | 150° | C. | 60° | D. | 30° |
分析 设经过两点$A({-1,\sqrt{3}})$,$B({1,-\sqrt{3}})$的直线的倾斜角为θ,利用斜率计算公式可得:tanθ=$\frac{\sqrt{3}-(-\sqrt{3})}{-1-1}$,解出即可得出.
解答 解:设经过两点$A({-1,\sqrt{3}})$,$B({1,-\sqrt{3}})$的直线的倾斜角为θ,
则tanθ=$\frac{\sqrt{3}-(-\sqrt{3})}{-1-1}$=-$\sqrt{3}$,
∵θ∈[0°,180°),
∴θ=120°.
故选:A.
点评 本题考查了直线的倾斜角与斜率的关系、三角函数求值,考查了推理能力与计算能力,属于基础题.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:解答题
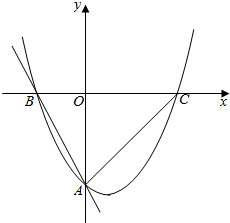 如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点
如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{x-1}$ | B. | y=2x-1 | C. | y=$\frac{1}{x-1}$ | D. | y=ln(x-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-3\sqrt{2},-\sqrt{2}})∪({\sqrt{2},3\sqrt{2}}]$ | B. | $({-3\sqrt{2},-\sqrt{2}}]∪[{\sqrt{2},3\sqrt{2}})$ | C. | $[{-3\sqrt{2},-\sqrt{2}}]∪[{\sqrt{2},3\sqrt{2}}]$ | D. | $({-3\sqrt{2},-\sqrt{2}})∪({\sqrt{2},3\sqrt{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
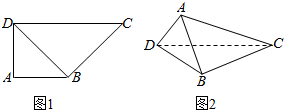 如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.
如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 2.125 | 2.25 | 2.375 | 2.5 | 2.625 | 2.75 | 2.875 | 3 |
| lgx | 0.301 | 0.327 | 0.352 | 0.376 | 0.398 | 0.419 | 0.439 | 0.459 | 0.477 |
| $\frac{1}{x}$ | 0.5 | 0.471 | 0.444 | 0.421 | 0.400 | 0.381 | 0.364 | 0.348 | 0.333 |
| A. | (2.125,2,25) | B. | (2.75,2.875) | C. | (2.625,2.75) | D. | (2.5,2.625) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 钝角三角形 | ||
| C. | 等腰非等边三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com