
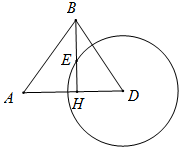
 如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其北偏东30°方向与它相距20海里的B处有一外国船只,且D岛位于海监船正东18海里处.
如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其北偏东30°方向与它相距20海里的B处有一外国船只,且D岛位于海监船正东18海里处.分析 (1)依题意,在△ABD中,∠DAB=60°,由余弦定理求得DB;
(2)法一、过点B作BH⊥AD于点H,在Rt△ABH中,求解直角三角形可得HE、AE的值,进一步得到sin∠EAH,则∠EAH可求,求出外国船只到达E处的时间t,由$v≥\frac{AE}{t}$求得速度的最小值.
法二、建立以点A为坐标原点,AD为x轴,过点A往正北作垂直的y轴.可得A,D,B的坐标,设经过t小时外国船到达点$E(10,10\sqrt{3}-4t)$,结合ED=12,得$E(10,4\sqrt{5})$,列等式求得t,则$tan∠EAD=\frac{EH}{AH}=\frac{{4\sqrt{5}}}{10}=\frac{{2\sqrt{5}}}{5}$,$∠EAD=arctan\frac{{2\sqrt{5}}}{5}≈{41.81°}$,再由$v≥\frac{AE}{t}$求得速度的最小值.
解答 解:(1)依题意,在△ABD中,∠DAB=60°,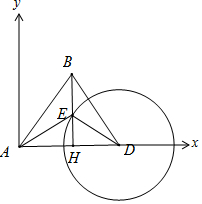
由余弦定理得DB2=AD2+AB2-2AD•AB•cos60°=182+202-2×18×15×cos60°=364,
∴$DB=2\sqrt{91}$,
即此时该外国船只与D岛的距离为$2\sqrt{91}$海里;
(2)法一、过点B作BH⊥AD于点H,
在Rt△ABH中,AH=10,∴HD=AD-AH=8,
以D为圆心,12为半径的圆交BH于点E,连结AE、DE,
在Rt△DEH中,HE=$\sqrt{E{D}^{2}-H{D}^{2}}=4\sqrt{5}$,∴$BE=10\sqrt{3}-4\sqrt{5}$,
又AE=$\sqrt{A{H}^{2}+H{E}^{2}}=6\sqrt{5}$,
∴sin∠EAH=$\frac{HE}{AE}=\frac{4\sqrt{5}}{6\sqrt{5}}=\frac{2}{3}$,则$∠EAH=arcsin\frac{2}{3}$≈41.81°.
外国船只到达点E的时间$t=\frac{BE}{4}=\frac{{5\sqrt{3}-2\sqrt{5}}}{2}≈2.09$(小时).
∴海监船的速度$v≥\frac{AE}{t}=\frac{{6\sqrt{5}}}{{\frac{{5\sqrt{3}-2\sqrt{5}}}{2}}}≈6.4$(海里/小时).
又90°-41.81°=48.2°,
故海监船的航向为北偏东48.2°,速度的最小值为6.4海里/小时.
法二、建立以点A为坐标原点,AD为x轴,过点A往正北作垂直的y轴.
则A(0,0),D(18,0),$B(10,10\sqrt{3})$,设经过t小时外国船到达点$E(10,10\sqrt{3}-4t)$,
又ED=12,得$E(10,4\sqrt{5})$,此时$t=\frac{{10\sqrt{3}-4\sqrt{5}}}{4}≈2.09$(小时).
则$tan∠EAD=\frac{EH}{AH}=\frac{{4\sqrt{5}}}{10}=\frac{{2\sqrt{5}}}{5}$,$∠EAD=arctan\frac{{2\sqrt{5}}}{5}≈{41.81°}$,
∴监测船的航向东偏北41.81°.
∴海监船的速度$v≥\frac{AE}{t}=\frac{{6\sqrt{5}}}{{\frac{{10\sqrt{3}-4\sqrt{5}}}{4}}}≈6.4$(海里/小时).
点评 本题是应用题,考查简单的数学建模思想方法,考查了直线与圆位置关系的应用,考查计算能力,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m、n不平行,则n与α不平行 | B. | 若m∥α,m、n不垂直,则n与α不垂直 | ||
| C. | 若m⊥α,m、n不平行,则n与α不垂直 | D. | 若m⊥α,m、n不垂直,则n与α不平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | (0,1) | D. | $({0,\frac{1}{2}})∪$$({\frac{1}{2},1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 13种 | C. | 14种 | D. | 15种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com