
分析 (1)根据对数的运算解不等式即可.
(2)根据f(0)=1,求f(x)的解析式,根据$f(x)={(\frac{1}{{\sqrt{2}}})^x}+λ$在闭区间[2,3]上有实数解,分离λ,可得λ=lg(x+10)-$(\frac{1}{\sqrt{2}})^{x}$,令F(x)=lg(x+10)-$(\frac{1}{\sqrt{2}})^{x}$,求在闭区间[2,3]上的值域即为λ的范围.
(3)函数f(x)的图象过点(98,2),求f(x)的解析式,可得f(x)=lg(2+x)那么:不等式f[cos(2nx)]<lg2转化为lg(2+cos(2nx))<lg2转化为$\left\{\begin{array}{l}{2+cos({2}^{n}x)>0}\\{cos({2}^{n}x)<0}\end{array}\right.$,求解x,又∵2+x>0,即x>-2和n∈N.讨论k的范围可得答案.
解答 解:函数f(x)=lg(x+m)(m∈R);
(1)当m=2时,f(x)=lg(x+2)
那么:不等式$f(\frac{1}{x})>1$;即lg($\frac{1}{x}$+2)>lg10,
可得:$\frac{1}{x}+2>10$,且$\frac{1}{x}+2>0$
解得:$0<x<\frac{1}{8}$.
∴不等式的解集为{x|$0<x<\frac{1}{8}$}
(2)∵f(0)=1,可得m=10.
∴f(x)=lg(x+10)
$f(x)={(\frac{1}{{\sqrt{2}}})^x}+λ$,即lg(x+10)=$(\frac{1}{\sqrt{2}})^{x}+λ$在闭区间[2,3]上有实数解,
可得λ=lg(x+10)-$(\frac{1}{\sqrt{2}})^{x}$
令F(x)=lg(x+10)-$(\frac{1}{\sqrt{2}})^{x}$,求在闭区间[2,3]上的值域.
根据指数和对数的性质可知:F(x)是增函数,
∴F(x)在闭区间[2,3]上的值域为[lg12-$\frac{1}{2}$,lg13-$\frac{\sqrt{2}}{4}$]
故得实数λ的范围是[lg12-$\frac{1}{2}$,lg13-$\frac{\sqrt{2}}{4}$].
(3)∵函数f(x)的图象过点(98,2),
则有:2=lg(98+m)
∴m=2.
故f(x)=lg(2+x)
那么:不等式f[cos(2nx)]<lg2转化为lg(2+cos(2nx))<lg2
即cos(2nx)<0对n∈N均成立,
若x是满足条件的实数,则有cosx≤-$\frac{1}{4}$,
因为,若-$\frac{1}{4}$<cosx<0,则cos2x=2cos2x-1<-$\frac{7}{8}$,则cos4x=2cos22x-1>0,
所以必有cos(2nx)≤-$\frac{1}{4}$;
得|cos(2nx)-$\frac{1}{2}$|≥$\frac{3}{4}$,又|cos2x+$\frac{1}{2}$|=2|cosx+$\frac{1}{2}$||cosx-$\frac{1}{2}$|≥$\frac{3}{2}$|cosx+$\frac{1}{2}$|,
得|cosx+$\frac{1}{2}$|≤$\frac{2}{3}$|cos2x+$\frac{1}{2}$|,重复运用得到|cosx+$\frac{1}{2}$|≤…≤$(\frac{2}{3})^{n}$|cos(2nx)+$\frac{1}{2}$|<$(\frac{2}{3})^{n}$
n为自然数,∴cosx+$\frac{1}{2}$=0,
级x=2kπ±$\frac{2π}{3}$,k∈Z.
验证,当x=2kπ±$\frac{2π}{3}$,k∈Z时,有cos(2nx)=-$\frac{1}{2}$,满足题意.
所以,x的取值范围为{x|x=2kπ±$\frac{2π}{3}$,k∈Z}
点评 本题考查了对数的性质及其运算以及不等式恒成立的问题在对数与三角函数中的运用.有点难度.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
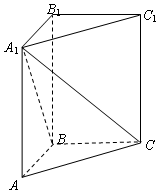 在正三棱柱ABC-A1B1C1中,AB=1,BB1=2,求:
在正三棱柱ABC-A1B1C1中,AB=1,BB1=2,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
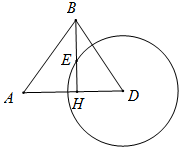 如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其北偏东30°方向与它相距20海里的B处有一外国船只,且D岛位于海监船正东18海里处.
如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其北偏东30°方向与它相距20海里的B处有一外国船只,且D岛位于海监船正东18海里处.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com