练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．已知x，y∈R+，且x+2y=1，则x•y的最大值为$\frac{1}{8}$．

    分析 直接利用基本不等式的性质即可得出．

    解答 解：x，y∈R+，
    x+2y=1，即1$≥2\sqrt{2xy}$，当且仅当x=2y=$\frac{1}{2}$时取等号．
    那么：$\frac{1}{4}≥2xy$，
    可得：xy$≤\frac{1}{8}$．
    ∴x•y的最大值为$\frac{1}{8}$．
    故答案为：$\frac{1}{8}$．

    点评 本题考查了基本不等式的性质的运用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    16．下列以x为自变量的函数中，是指数函数的是（　　）
    A．$\begin{array}{l}\\ y={3^x}\end{array}$B．y=（-3）xC．y=2x+1D．y=x3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．某奶茶店的日销售收入y（单位：百元）与当天平均气温x（单位：℃）之间的关系如下：
    x-2-1012
    y5221
    通过上面的五组数据得到了x与y之间的线性回归方程：$\stackrel{∧}{y}$=-x+2.8；但现在丢失了一个数据，该数据应为（　　）
    A．3B．4C．5D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．设a∈R，则“a=1”是“复数（a-1）（a+2）+（a+3）i为纯虚数”的（　　）
    A．充分非必要条件B．必要非充分条件
    C．充要条件D．既非充分又非必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．设函数f（x）=lg（x+m）（m∈R）；
    （1）当m=2时，解不等式$f（\frac{1}{x}）＞1$；
    （2）若f（0）=1，且$f（x）={（\frac{1}{{\sqrt{2}}}）^x}+λ$在闭区间[2，3]上有实数解，求实数λ的范围；
    （3）如果函数f（x）的图象过点（98，2），且不等式f[cos（2nx）]＜lg2对任意n∈N均成立，求实数x的取值集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知AB为单位圆O的一条弦，P为单位圆O上的点．若f（λ）=|$\overrightarrow{AP}$-λ$\overrightarrow{AB}$|（λ∈R）的最小值为m，当点P在单位圆上运动时，m的最大值为$\frac{4}{3}$，则线段AB的长度为$\frac{4\sqrt{2}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．数列{an}是首项为1，公差为2的等差数列，Sn是它前n项和，则$\lim_{n→∞}\frac{S_n}{a_n^2}$=$\frac{1}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．函数$f（x）=1-3{sin^2}（{x+\frac{π}{4}}）$的最小正周期为π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

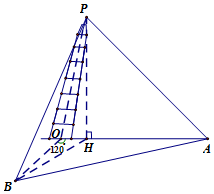    16．上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”．兴趣小组同学实施如下方案来测量塔的倾斜度和塔高：如图，记O点为塔基、P点为塔尖、点P在地面上的射影为点H．在塔身OP射影所在直线上选点A，使仰角k∠HAP=45°，过O点与OA成120°的地面上选B点，使仰角∠HPB=45°（点A、B、O都在同一水平面上），此时测得∠OAB=27°，A与B之间距离为33.6米．试求：
    （1）塔高（即线段PH的长，精确到0.1米）；
    （2）塔身的倾斜度（即PO与PH的夹角，精确到0.1°）．

    查看答案和解析>>

    同步练习册答案