
分析 由直线AB平行于平面EFGH,且平面ABC交平面EFGH于HG,所以HG∥AB,同理EF∥AB,FG∥CD,EH∥CD,所以FG∥EH,EF∥HG.四边形EFGH为平行四边形.又AD=BD,AC=BC的对称性,可知AB⊥CD.
所以:四边形EFGH为矩形.建立二次函数关系求解四边形EFGH面积的最大值.
解答 解:∵直线AB平行于平面EFGH,且平面ABC交平面EFGH于HG,∴HG∥AB;
同理:EF∥AB,FG∥CD,EH∥CD,所以:FG∥EH,EF∥HG.
故:四边形EFGH为平行四边形.
又∵AD=BD,AC=BC的对称性,可知AB⊥CD.
所以:四边形EFGH为矩形.
设BF:BD=BG:BC=FG:CD=x,(0≤x≤1)
FG=2$\sqrt{2}$x,HG=2$\sqrt{2}$(1-x)
SEFGH=FG×HG=8x(1-x)=-8(x-$\frac{1}{2}$)2+2,
根据二次函数的性质可知:SEFGH面积的最大值2.
故答案为2.
点评 本题考查了四面体ABCD中的对称性来证明四边形是矩形.同时考查了动点的问题以及灵活性的运用.属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
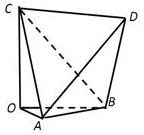 如图,多面体OABCD,AB=CD=2,AD=BC=$2\sqrt{3}$,AC=BD=$\sqrt{10}$,且OA,OB,OC两两垂直,则下列说法正确的是( )
如图,多面体OABCD,AB=CD=2,AD=BC=$2\sqrt{3}$,AC=BD=$\sqrt{10}$,且OA,OB,OC两两垂直,则下列说法正确的是( )| A. | 直线OB∥平面ACD | |
| B. | 球面经过点A、B、C、D四点的球的直径是$\sqrt{13}$ | |
| C. | 直线AD与OB所成角是45° | |
| D. | 二面角A-OC-D等于30° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
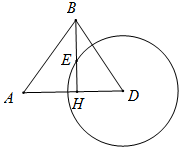 如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其北偏东30°方向与它相距20海里的B处有一外国船只,且D岛位于海监船正东18海里处.
如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其北偏东30°方向与它相距20海里的B处有一外国船只,且D岛位于海监船正东18海里处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com