
分析 可设△ABC的三边分别为a=3,b=5,c=7,运用余弦定理可得cosC,由同角的平方关系可得sinC,再由正弦定理可得该三角形的外接圆半径为$\frac{c}{2sinC}$,代入计算即可得到所求值.
解答 解:可设△ABC的三边分别为a=3,b=5,c=7,
由余弦定理可得,cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{9+25-49}{2×3×5}$=-$\frac{1}{2}$,
可得sinC=$\sqrt{1-co{s}^{2}C}$=$\sqrt{1-\frac{1}{4}}$=$\frac{\sqrt{3}}{2}$,
可得该三角形的外接圆半径为$\frac{c}{2sinC}$=$\frac{7}{2×\frac{\sqrt{3}}{2}}$=$\frac{7\sqrt{3}}{3}$.
故答案为:$\frac{7\sqrt{3}}{3}$.
点评 本题考查三角形的外接圆的半径的求法,注意运用正弦定理和余弦定理,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
 某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图,图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃,下面叙述不正确的是( )
某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图,图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃,下面叙述不正确的是( )| A. | 各月的平均最低气温都在0℃以上 | |
| B. | 七月的平均温差比一月的平均温差大 | |
| C. | 三月和十一月的平均最高气温基本相同 | |
| D. | 平均最高气温高于20℃的月份有5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1>0,0.6<q<0.7 | B. | a1<0,-0.7<q<-0.6 | ||
| C. | a1>0,0.7<q<0.8 | D. | a1<0,-0.8<q<-0.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -$\sqrt{3}$+2 | C. | -$\sqrt{3}$-2 | D. | $\sqrt{3}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
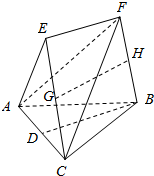 在如图所示的几何体中,D是AC的中点,EF∥DB.
在如图所示的几何体中,D是AC的中点,EF∥DB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$-y2=1 | B. | x2-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{3{x}^{2}}{20}$-$\frac{3{y}^{2}}{5}$=1 | D. | $\frac{3{x}^{2}}{5}$-$\frac{{3y}^{2}}{20}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com