
| x |
科目:高中数学 来源: 题型:
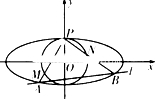 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
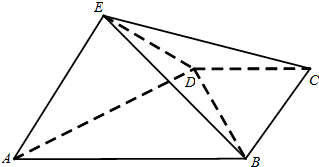 如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.
如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.查看答案和解析>>
科目:高中数学 来源: 题型:
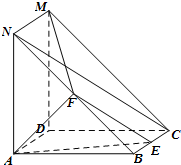 如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点.
如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点.| BE |
| BC |
查看答案和解析>>
科目:高中数学 来源: 题型:
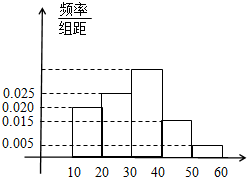 “你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了100名年龄段在[10,20),[20,30),…,[50,60)的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
“你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了100名年龄段在[10,20),[20,30),…,[50,60)的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 1 |
| an•an+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com