
【题目】已知f(x)是定义在R上的奇函数,当x≤0时,f(x)=x(2+x).
(1)求函数f(x)的解析式;
(2)画出函数f(x)的图象,并写出单调区间.
【答案】
(1)解:设x>0,则﹣x<0,
∵当x≤0时,f(x)=x(2+x),
∴f(﹣x)=﹣x(2﹣x).
又f(x)是定义在R上的奇函数,即f(﹣x)=﹣f(x),
∴当x>0时,f(x)=x(2﹣x).
故函数f(x)的解析式为 ![]()
(2)解:
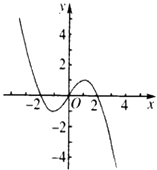
函数f(x)的单调递增区间为[﹣1,1],单调递减区间为(﹣∞,﹣1)和(1,+∞).
【解析】(1)当x>0,则﹣x<0,由已知表达式可求得f(﹣x),由奇函数的性质可得f(x)与f(﹣x)的关系,从而可求出f(x);(2)根据函数的解析式,得出函数f(x)的图象,从而写出单调区间.
【考点精析】根据题目的已知条件,利用函数奇偶性的性质的相关知识可以得到问题的答案,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点. 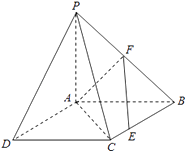
(1)求证:AF⊥EF;
(2)求二面角A﹣PC﹣B的平面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E、F分别是PA、PC的中点. 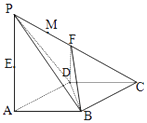
(Ⅰ)证明:PA∥平面FBD;
(Ⅱ)若PA=1,在棱PC上是否存在一点M使得二面角E﹣BD﹣M的大小为60°.若存在,求出PM的长,不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x2+2(a﹣1)x+2在区间[﹣1,2]上单调,则实数a的取值范围为( )
A.[2,+∞)
B.(﹣∞,﹣1]
C.(﹣∞,﹣1]∪[2,+∞)
D.(﹣∞,﹣1)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() +
+ ![]() 的定义域为( )
的定义域为( )
A.{x|x≥﹣3且x≠﹣2}
B.{x|x≥﹣3且x≠2}
C.{x|x≥﹣3}
D.{x|x≥﹣2且x≠3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .直线
.直线![]() 交曲线
交曲线![]() 于
于![]() 两点.
两点.
(1)写出直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,求点
,求点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=  .
.
(1)画出函数f(x)图象;
(2)求f(﹣a2﹣1)(a∈R),f(f(3))的值;
(3)当﹣4≤x<3时,求f(x)取值的集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com