练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
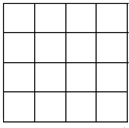
    8．将“丹、东、市”填入如图所示的4×4小方格内，每格内只填入一个汉字，且任意两个汉字既不同行也不同列，则不同的填写方法有（　　）
    A．288B．144C．576D．96

    分析 由题意知本题用分步计数原理，先从16个格子中任选一格放一个汉字，3个汉字既不同行也不同列，剩下的只有9个格子可以放，只有4个格子可以放，根据分步计数原理得到结果．

    解答 解：由题意知本题用分步计数原理，
    第一步先从16个格子中任选一格放一个汉字有16中方法，
    第二步3个棋子既不同行也不同列，剩下的只有9个格子可以放有9种方法，
    第三步只有4个格子可以放，有4种方法，
    由分步计数原理知共有16×9×4=576，
    故选：C．

    点评 本题应用计数原理解决，必须且只需连续完成这3个步骤，这件事才算完成．用两个计数原理解决计数问题时，最重要的是在开始计算之前要进行仔细分析要完成的“一件事”是什么，可以“分类”还是需要“分步”．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．已知$tanθ=\frac{1}{3}$，则$sin（{\frac{3}{2}π+2θ}）$的值为（　　）
    A．$-\frac{4}{5}$B．$-\frac{1}{5}$C．$\frac{1}{5}$D．$\frac{4}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设$a={2^{\frac{1}{3}}}，b={log_4}3，c={log_8}5$，则（　　）
    A．a＞b＞cB．a＞c＞bC．c＞a＞bD．b＞c＞a

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．如图，在正方体ABCD-A1B1C1D1中．
    求证：
    （1）A1C⊥BD；
    （2）平面AB1D1∥平面BC1D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．下面说法不正确的选项（　　）
    A．函数的单调区间可以是函数的定义域
    B．函数的多个单调增区间的并集也是其单调增区间
    C．具有奇偶性的函数的定义域定关于原点对称
    D．关于原点对称的图象一定是奇函数的图象

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数$f（x）=a-\frac{1}{x}$是定义在（0，+∞）上的函数．
    （1）求证：函数y=f（x）在（0，+∞）上是增函数；
    （2）若函数y=f（x）在[m，n]上的值域是[2m，2n]（m＜n），求实数a的取值范围；
    （3）若不等式x2|f（x）|≤1对$x∈[{\frac{1}{3}，\frac{1}{2}}]$恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

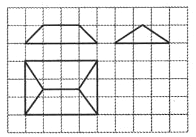    20．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：今有刍童，下广三丈，袤四丈，上袤二丈，无广，高一丈，问：积几何？其意思是说：“今有底面为矩形的屋脊状楔体，下底面宽3丈，长4丈；上棱长2丈，高一丈．问它的体积是多少？”已知一丈为10尺，现将该楔体的三视图给出如右图所示，其中网格纸上小正方形的边长为1，则该楔体的体积为（　　）
    A．5000立方尺B．5500立方尺C．6000立方尺D．6500立方尺

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．i表示虚数单位，则1+i1+i2+…+i2014=i．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

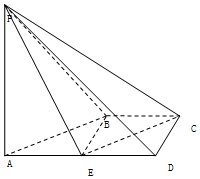    18．如图，在四棱锥P-ABCD中，AD∥BC，∠ADC=∠PAB=90°，BC=CD=$\frac{1}{2}$AD，E为棱AD的中点，异面直线PA与CD所成的角为90°．
    （Ⅰ）证明：CD⊥平面PAD；
    （Ⅱ）若二面角P-CD-A的大小为45°，求直线PA与平面PCE所成角的正弦值．

    查看答案和解析>>

    同步练习册答案