
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆上一点
,且椭圆上一点![]() 与椭圆左右两个焦点构成的三角形周长为
与椭圆左右两个焦点构成的三角形周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
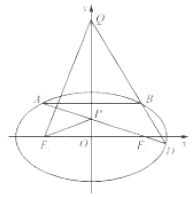
(2)如图,设点![]() 为椭圆上任意一点,直线
为椭圆上任意一点,直线![]() 和椭圆
和椭圆![]() 交于
交于![]() 两点,且直线
两点,且直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 两点,求证:
两点,求证: ![]() .
.
【答案】(1) ![]() ;(2)详见解析.
;(2)详见解析.
【解析】试题分析:(1)由![]() ,又
,又![]() ,联立求出
,联立求出![]() 、
、![]() 、
、![]() 的值,即可得出椭圆
的值,即可得出椭圆![]() 的方程;(2)设
的方程;(2)设![]() ,则
,则![]() ,求出直线
,求出直线![]() 的方程与直线
的方程与直线![]() 方程,可得
方程,可得![]() 的坐标,利用斜率公式只要证明
的坐标,利用斜率公式只要证明![]() 即可得出结果.
即可得出结果.
试题解析:∵![]() ,∴
,∴![]()
![]()
∴![]()
∴椭圆方程为![]()
(2)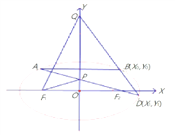
设![]() ,则
,则![]() ,
,
直线![]() 方程为
方程为![]()
令![]() ,则
,则![]()
∴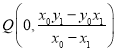
同理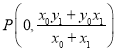
∵![]() 和
和![]() 均为锐角,
均为锐角,
∴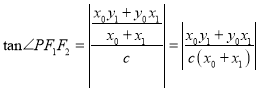
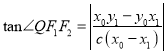
∴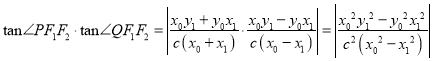
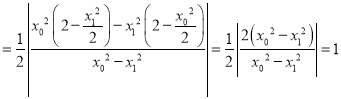
∴![]() 与
与![]() 互余,
互余,
∴![]()
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如果函数f(x)=3sin(2x+φ)的图象关于点( ![]() ,0)成中心对称(|φ|<
,0)成中心对称(|φ|< ![]() ),那么函数f(x)图象的一条对称轴是( )
),那么函数f(x)图象的一条对称轴是( )
A.x=﹣ ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B,C,D为平面内的四点,且A(1,3),B(2,﹣2),C(4,1).
(1)若 ![]() =
= ![]() ,求D点的坐标;
,求D点的坐标;
(2)设向量 ![]() =
= ![]() ,
, ![]() =
= ![]() ,若k
,若k ![]() ﹣
﹣ ![]() 与
与 ![]() +3
+3 ![]() 平行,求实数k的值.
平行,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】漳州市“网约车”的现行计价标准是:路程在2km以内(含2km)按起步价8元收取,超过2km后的路程按1.9元/km收取,但超过10km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85元).
(1)将某乘客搭乘一次“网约车”的费用f(x)(单位:元)表示为行程x(0<x≤60,单位:km)的分段函数;
(2)某乘客的行程为16km,他准备先乘一辆“网约车”行驶8km后,再换乘另一辆“网约车”完成余下行程,请问:他这样做是否比只乘一辆“网约车”完成全部行程更省钱?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的倾斜角为45°,以坐标原点为极点,
的倾斜角为45°,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 和曲线
和曲线![]() 的交点为点
的交点为点![]() .
.
(1)求直线![]() 的参数方程;
的参数方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=﹣ ![]() x3+x2+(m2﹣1)x,(x∈R),其中m>0.
x3+x2+(m2﹣1)x,(x∈R),其中m>0.
(1)当m=1时,曲线y=f(x)在点(1,f(1))处的切线斜率;
(2)求函数的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为( )(结果保留一位小数.参考数据:![]() ,
,![]() )( )
)( )
A. 1.3日 B. 1.5日 C. 2.6日 D. 2.8日
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com