
【题目】如果函数f(x)=3sin(2x+φ)的图象关于点( ![]() ,0)成中心对称(|φ|<
,0)成中心对称(|φ|< ![]() ),那么函数f(x)图象的一条对称轴是( )
),那么函数f(x)图象的一条对称轴是( )
A.x=﹣ ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PD⊥底面ABCD,点M、N分别是棱AB、CD的中点. 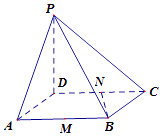
(1)证明:BN⊥平面PCD;
(2)在线段PC上是否存在点H,使得MH与平面PCD所成最大角的正切值为 ![]() ,若存在,请求出H点的位置;若不存在,请说明理由.
,若存在,请求出H点的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx+c,其对称轴为y轴(其中b,c为常数) (Ⅰ)求实数b的值;
(Ⅱ)记函数g(x)=f(x)﹣2,若函数g(x)有两个不同的零点,求实数c的取值范围;
(Ⅲ)求证:不等式f(c2+1)>f(c)对任意c∈R成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2+ax+a)e﹣x , (a为常数,e为自然对数的底).
(1)当a=0时,求f′(2);
(2)若f(x)在x=0时取得极小值,试确定a的取值范围;
(3)在(2)的条件下,设由f(x)的极大值构成的函数为g(a),将a换元为x,试判断曲线y=g(x)是否能与直线3x﹣2y+m=0(m为确定的常数)相切,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 50 | 60 | 70 |
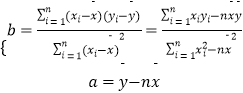
(1)画出散点图;
(2)求线性回归方程;
(3)预测当广告费支出为7百万元时的销售额.参考公式:.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆上一点
,且椭圆上一点![]() 与椭圆左右两个焦点构成的三角形周长为
与椭圆左右两个焦点构成的三角形周长为![]() .
.
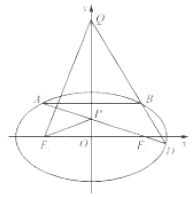
(1)求椭圆![]() 的方程;
的方程;
(2)如图,设点![]() 为椭圆上任意一点,直线
为椭圆上任意一点,直线![]() 和椭圆
和椭圆![]() 交于
交于![]() 两点,且直线
两点,且直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 两点,求证:
两点,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com