
分析 (1)f(7)=(a+b)7,二、三、四项的二项式系数为7,21,35,依次成等差数列,可得结论;
(2)由题意,2Cnr=Cnr-1+Cnr+1,整理可得4r(n-r)=(n-2)(n+1),可得(n-2)(n+1)能被4整除,从而n-2或n+1为偶数时,必须能被4整除,结合n≤2015,即可求n的最大值.
解答 (1)证明:f(7)=(a+b)7,二、三、四项的二项式系数为7,21,35,依次成等差数列,
所以f(7)具有性质P.
(2)解:由题意,2Cnr=Cnr-1+Cnr+1,
整理可得4r(n-r)=(n-2)(n+1),
∴(n-2)(n+1)能被4整除,
∵n-2、n+1一奇一偶,
∴n-2或n+1为偶数时,必须能被4整除,
∵n≤2015
∴n的最大值为2012.
点评 本题考查二项式定理的运用,考查学生对定义的理解,考查学生分析解决问题的能力,属于中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:选择题
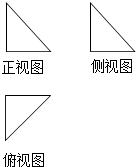
| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
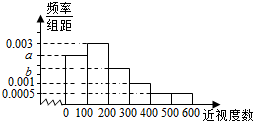 某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:| 近视度数 | 0-100 | 100-200 | 200-300 | 300-400 | 400以上 |
| 学生频数 | 30 | 40 | 20 | 10 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com