Question

18．在60°的二面角α-l-β的棱l上有两点A，B，直线AC，BD分别在这个二面角的两个半平面内，AC⊥l．BD⊥l，若AB=4，AC=6，BD=8，则CD的长为2$\sqrt{17}$．

Answer 1

分析 利用已知条件确定＜$\overrightarrow{CA\;}，\overrightarrow{BD\;}$＞120°，利用$|\overrightarrow{CD\;}{|^2}$=${（\overrightarrow{CA\;}+\overrightarrow{AB\;}+\overrightarrow{BD\;}）^2}$，通过向量的数量积的运算求出CD的距离．

解答 解：由已知，可得AC⊥AB，BD⊥AB，
∵二面角的大小为60°，
则＜$\overrightarrow{AC}$，$\overrightarrow{BD}$＞=60°．
∴＜$\overrightarrow{CA\;}，\overrightarrow{BD\;}$＞=120°，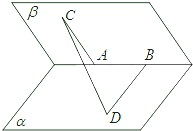
∴$|\overrightarrow{CD\;}{|^2}$=${（\overrightarrow{CA\;}+\overrightarrow{AB\;}+\overrightarrow{BD\;}）^2}$
=$|\overrightarrow{CA\;}{|^2}$+$|\overrightarrow{AB\;}{|^2}$+$|\overrightarrow{BD\;}{|^2}$+2$\overrightarrow{CA\;}•\overrightarrow{AB\;}$+2$\overrightarrow{CA\;}•\overrightarrow{BD\;}$+2$\overrightarrow{AB\;}•\overrightarrow{BD\;}$
=36+16+64+2×6×8×cos120°=68．
∴$CD=\sqrt{68}$=2$\sqrt{17}$．                                
故答案为：2$\sqrt{17}$

点评 本题考查空间两点间的距离的求法，空间向量的数量积的应用，根据二面角的大小转化为向量的夹角关系是解决本题的关键．