
分析 由二次函数图象可得,关于x的不等式x2+2ax+4>0对一切x∈R恒成立必有△=4a2-16<0可得P;由函数f(x)=-(5-2a)x是减函数可得5-2a>1可得q,求出p,q 两个为假是的a,利用补集的思想即可求出a.
解答 解:由关于x的不等式x2+2ax+4>0对一切x∈R恒成立可得△=4a2-16<0,∴命题P:-2<a<2
由函数f(x)=-(5-2a)x是减函数可得5-2a>1,则a<2∴命题q:a<2.
若命题“p、q”均为假命题时,
$\left\{\begin{array}{l}{a≥2或a≤-2}\\{a≥2}\end{array}\right.$⇒a≥2.
所以实数a的取值范围:[2,+∞)
点评 本题主要考查了p或q复合命题的真假的应用,解题的关键是利用二次函数的性质及指数函数的单调性准确求出命题p,q为真时a的范围,同时也考查了补集的思想,属于中档题.


科目:高中数学 来源: 题型:解答题
 随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题.某汽车销售公司作了一次抽样调查,并统计得出某款车的使用年限x与所支出的总费用y(万元)有如表的数据资料:
随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题.某汽车销售公司作了一次抽样调查,并统计得出某款车的使用年限x与所支出的总费用y(万元)有如表的数据资料:| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 总费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
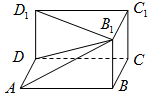 长方体ABCD-A1B1C1D1被挖去一个四棱锥后如图所示.已知AB=5,BC=4,BB=3.
长方体ABCD-A1B1C1D1被挖去一个四棱锥后如图所示.已知AB=5,BC=4,BB=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
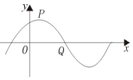 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,其中点P(1,2)为函数图象的一个最高点,Q(4,0)为函数图象与x轴的一个交点,O为坐标原点.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,其中点P(1,2)为函数图象的一个最高点,Q(4,0)为函数图象与x轴的一个交点,O为坐标原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com