练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．解方程
    （1）9-x-2•31-x=27
    （2）log4（3-x）+log0.25（3+x）=log4（1-x）+log0.25（2x+1）

    分析 （1）方程转化为3-x的二次方程，然后分解因式，求出解，利用指数的性质求解即可．
    （2）利用对数的运算法则，化简对数方程，转化分式方程，求解即可．

    解答 解：（1）（3-x）2-6•3-x-27=0，化为（3-x+3）（3-x-9）=0，
    而3-x+3≠0，∴3-x-9=0，即3-x=32，解得x=-2
    （2）log4（3-x）+log0.25（3+x）=log4（1-x）+log0.25（2x+1）${log_4}\frac{3-x}{1-x}={log_{0.25}}\frac{2x+1}{3+x}={log_4}\frac{x+3}{2x+1}$，$\frac{3-x}{1-x}=\frac{x+3}{2x+1}$，得x=7或x=0，经检验x=0为所求

    点评 本题考查函数的零点与方程根的解法，考查计算能力，注意根的检验．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．已知命题p：对?x∈R，x2-x-1≥0恒成立．命题q：?x∈R是2x-1≤0成立．则下列命题中为真命题的是（　　）
    A．（?p）∧qB．（?p）∧（?q）C．p∧（?q）D．p∧q

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．求函数y=$\frac{{x}^{2}+3}{{x}^{2}+2}$的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．f（x）=（$\frac{1}{2}$）x-x+1，用二分法求方程（$\frac{1}{2}$）x-x+1=0在（0，3）内近似解的过程中，f（1）＞0，f（1.5）＜0，f（2）＜0，f（3）＜0，则方程的根落在区间（　　）
    A．（1，1.5）B．（1.5，2）C．（2，3）D．无法确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．下列四个命题中，
    ①?x∈R，2x-1＞0
    ②?x∈N*，（x-1）2＞0
    ③?x0∈Z，y0∈Z，使3x0-2y0=10
    真命题的个数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知f（x）=（k-2）x2+（k-1）x+3是偶函数，则k=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．设x，y满足约束条件$\left\{\begin{array}{l}x+y+5≥0\\ x-y≤0\\ y≤0\end{array}\right.$，求目标函数Z=2x+4y的最小值和最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．cos（-30°）的值是（　　）
    A．$-\frac{1}{2}$B．$\frac{1}{2}$C．$-\frac{{\sqrt{3}}}{2}$D．$\frac{{\sqrt{3}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

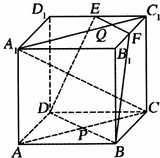    3．如图：在正方体ABCD-A1B1C1D1中，E，F分别为D1C1，B1C1的中点，AC∩BD=P，A1C1∩EF=Q，直线A1C与平面BDEF的交点为R．
    （1）证明：B，D，F，E四点共面；
    （2）证明：P，Q，R三点共线；
    （3）证明：DE，BF，CC1三线共点．

    查看答案和解析>>

    同步练习册答案