练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，a=2，A=45°，若此三角形有两解，则b的取值范围是（ ）
    A.（2，2 ）
    B.（2，+∞）
    C.（﹣∞，2）
    D.（ ， ）

    【答案】A
    【解析】解：∵a=2，A=45°， ∴由正弦定理可得： ，解得b=2 sinB，
    ∵B+C=180°﹣45°=135°，由B有两个值，则这两个值互补，
    若B≤45°，
    则和B互补的角大于135°，这样A+B＞180°，不成立，
    ∴45°＜B＜135°，
    又若B=90°，这样补角也是90°，一解，
    所以 ＜sinB＜1，
    b=2 sinB，
    所以2＜b＜2 ．
    则b的取值范围是为：（2，2 ）．
    故选：A．
    【考点精析】本题主要考查了正弦定理的定义的相关知识点，需要掌握正弦定理:才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足a1=3，an+1﹣3an=3n（n∈N*），数列{bn}满足bn= ．
    （Ⅰ）求证：数列{bn}是等差数列，并求数列{an}的通项公式；
    （Ⅱ）求数列{an}的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正三棱柱ABC﹣A1B1C1的棱长都为2，E，F，G为 AB，AA1 ， A1C1的中点，则B1F 与面GEF成角的正弦值（ ）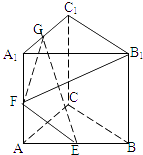

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（ sin ，1）， =（cos ，cos2 ）．
    （Ⅰ）若 =1，求cos（ ﹣x）的值；
    （Ⅱ）记f（x）= ，在△ABC中，A、B、C的对边分别为a、b、c，且满足（2a﹣c）cosB=bcosC，求函数f（A）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校为评估新教改对教学的影响，挑选了水平相当的两个平行班进行对比试验。甲班采用创新教法，乙班仍采用传统教法，一段时间后进行水平测试，成绩结果全部落在区间内（满分100分），并绘制频率分布直方图如右图，两个班人数均为60人，成绩80分及以上为优良。

    根据以上信息填好下列联表，并判断出有多大的把握认为学生成绩优良与班级有关？

    （2）以班级分层抽样,抽取成绩优良的5人参加座谈，现从5人中随机选3人来作书面发言，求发言人至少有2人来自甲班的概率。

    (以下临界值及公式仅供参考

    , )

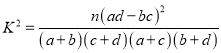    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=log2（1+x）﹣log2（1﹣x），g（x）=log2（1+x）+log2（1﹣x）．
    （1）判断函数f（x）奇偶性并证明；
    （2）判断函数f（x）单调性并用单调性定义证明；
    （3）求函数g（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左右焦点为，其离心率为，又抛物线在点处的切线恰好过椭圆的一个焦点.

    （1）求椭圆的方程；

    （2）过点斜率为的直线交椭圆于两点，直线的斜率分别为，是否存在常数，使得？若存在，求出的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的几何体，关于其结构特征，下列说法不正确的是（　　）

    A.该几何体是由两个同底的四棱锥组成的几何体
    B.该几何体有12条棱、6个顶点
    C.该几何体有8个面，并且各面均为三角形
    D.该几何体有9个面，其中一个面是四边形，其余均为三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】阅读如图所示的程序框图，运行相应的程序，则输出的s值等于 ．

    查看答案和解析>>

    同步练习册答案