
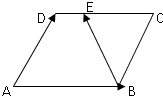
 在边长为1的菱形ABCD中,∠A=60°,E是线段CD上一点,满足|$\overrightarrow{CE}$|=2||$\overrightarrow{DE}$|,如图所示,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
在边长为1的菱形ABCD中,∠A=60°,E是线段CD上一点,满足|$\overrightarrow{CE}$|=2||$\overrightarrow{DE}$|,如图所示,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.分析 (1)根据向量加、减法运算法则计算即可;
(2)设$\overrightarrow{BF}=t\overrightarrow{BC}=t\overrightarrow{b}$,则$\overrightarrow{FC}=(1-t)\overrightarrow{b}$,(0≤t≤1),$\overrightarrow{AF}$=$\overrightarrow{a}+t\overrightarrow{b}$,利用$|\overrightarrow{a}|=|\overrightarrow{b}|=1$、$\overrightarrow{a}•\overrightarrow{b}$=$\frac{1}{2}$及$\overrightarrow{AF}$•$\overrightarrow{BE}$=0,计算即可.
解答 解:(1)根据题意得:$\overrightarrow{BC}=\overrightarrow{AD}=\overrightarrow{b}$,
$\overrightarrow{CE}=\frac{2}{3}\overrightarrow{CD}=\frac{2}{3}\overrightarrow{BA}=-\frac{2}{3}\overrightarrow{AB}=-\frac{2}{3}\overrightarrow{a}$,
∴$\overrightarrow{BE}$=$\overrightarrow{BC}+\overrightarrow{CE}$=$\overrightarrow{b}-\frac{2}{3}\overrightarrow{a}$; (2)结论:在线段BC上存在使得$4|\overrightarrow{BF}|=|\overrightarrow{BC}|$的一点F满足AF⊥BE,此时|$\overrightarrow{AF}$|=$\frac{\sqrt{21}}{4}$.
(2)结论:在线段BC上存在使得$4|\overrightarrow{BF}|=|\overrightarrow{BC}|$的一点F满足AF⊥BE,此时|$\overrightarrow{AF}$|=$\frac{\sqrt{21}}{4}$.
理由如下:
设$\overrightarrow{BF}=t\overrightarrow{BC}=t\overrightarrow{b}$,则$\overrightarrow{FC}=(1-t)\overrightarrow{b}$,(0≤t≤1),
∴$\overrightarrow{AF}$=$\overrightarrow{AB}+\overrightarrow{BF}$=$\overrightarrow{a}+t\overrightarrow{b}$,
∵在边长为1的菱形ABCD中,∠A=60°,
∴$|\overrightarrow{a}|=|\overrightarrow{b}|=1$,$\overrightarrow{a}•\overrightarrow{b}$=$|\overrightarrow{a}||\overrightarrow{b}|cos60°$=$\frac{1}{2}$,
∵AF⊥BE,
∴$\overrightarrow{AF}$•$\overrightarrow{BE}$=($\overrightarrow{a}+t\overrightarrow{b}$)•($\overrightarrow{b}-\frac{2}{3}\overrightarrow{a}$)
=$(1-\frac{2}{3}t)$$\overrightarrow{a}•\overrightarrow{b}$-$\frac{2}{3}{\overrightarrow{a}}^{2}$+$t{\overrightarrow{b}}^{2}$
=$(1-\frac{2}{3}t)$×$\frac{1}{2}$-$\frac{2}{3}$+t
=0,
解得t=$\frac{1}{4}$,从而$\overrightarrow{AF}$=$\overrightarrow{a}+\frac{1}{4}\overrightarrow{b}$,
∴$|\overrightarrow{AF}|$=$\sqrt{{\overrightarrow{AF}}^{2}}$=$\sqrt{{\overrightarrow{a}}^{2}+\frac{1}{2}\overrightarrow{a}•\overrightarrow{b}+\frac{1}{16}{\overrightarrow{b}}^{2}}$=$\sqrt{1+\frac{1}{2}•\frac{1}{2}+\frac{1}{16}}$=$\frac{\sqrt{21}}{4}$.
点评 本题考查向量的加、减法运算法则,数量积运算,将线段垂直转化为向量垂直是解决本题的关键,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD是平行四边形,∠DAB=60°,AB=2AD=2,PD⊥平面ABCD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,∠DAB=60°,AB=2AD=2,PD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | -$\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,4) | B. | [-2,4) | C. | (0,2) | D. | (0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 8 | C. | $2\sqrt{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com