
分析 (1)由不满足f($\frac{π}{4}$+x)≠f($\frac{π}{4}$-x)(x∈R),得f(x)=sin$\frac{4}{3}$x不是“M函数”,
(2)可得函数f(x)的周期T=$\frac{3π}{2}$,f(x)=f($\frac{π}{2}$-x)(x∈R),
①当x$∈[\frac{3}{2}kπ+\frac{π}{4},\frac{3}{2}kπ+π]$时,f(x)=f(x-$\frac{3}{2}kπ$)=sin(x-$\frac{3}{2}kπ$)
②当x∈[$\frac{3}{2}kπ-\frac{π}{2},\frac{3}{2}kπ+\frac{π}{4}$]时,f(x)=f[$\frac{π}{2}$-(x-$\frac{3}{2}kπ$)]=cos(x-$\frac{3}{2}kπ$)
在[0,$\frac{3π}{2}$]上的单调递增区间:[$\frac{π}{4}$,$\frac{π}{2}$],[π,$\frac{3π}{2}$]
(3)由(2)可得函数f(x)在[-$\frac{π}{2}$,π]上的图象,根据图象可得:
①当0$≤a<\frac{\sqrt{2}}{2}$或1时,f(x)=a(a为常数)有2个解,其和为$\frac{π}{2}$
②当a=$\frac{\sqrt{2}}{2}$时,f(x)=a(a为常数)有3个解,其和为$\frac{3}{4}π$.
③当$\frac{\sqrt{2}}{2}<a<1$时,f(x)=a(a为常数)有4个解,其和为π
即可得当x∈[-$\frac{π}{2}$,$\frac{3kπ}{2}$+π](k∈N)时,记关于x的方程f(x)=a(a为常数)所有解的和为S(k),
解答 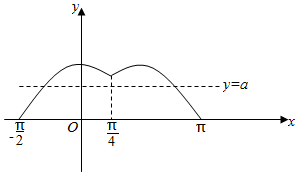 解:(1)f(x)=sin$\frac{4}{3}$x不是“M函数”.
解:(1)f(x)=sin$\frac{4}{3}$x不是“M函数”.
∵f($\frac{π}{4}$+x)=sin$\frac{4}{3}(\frac{π}{4}+x)$=sin($\frac{π}{3}+\frac{4}{3}x$),f($\frac{π}{4}$-x)=sin$\frac{4}{3}(\frac{π}{4}-x)$=sin($\frac{π}{3}$-$\frac{4}{3}$x)
∴f($\frac{π}{4}$+x)≠f($\frac{π}{4}$-x)(x∈R),
∴f(x)=sin$\frac{4}{3}$x不是“M函数”.
(2)∵函数f(x)满足f(x)=f(x+$\frac{3π}{2}$),∴函数f(x)的周期T=$\frac{3π}{2}$
∵f($\frac{π}{4}$+x)=f($\frac{π}{4}$-x)(x∈R),∴f(x)=f($\frac{π}{2}$-x)(x∈R),
①当x$∈[\frac{3}{2}kπ+\frac{π}{4},\frac{3}{2}kπ+π]$时,f(x)=f(x-$\frac{3}{2}kπ$)=sin(x-$\frac{3}{2}kπ$)
②当x∈[$\frac{3}{2}kπ-\frac{π}{2},\frac{3}{2}kπ+\frac{π}{4}$]时,f(x)=f[$\frac{π}{2}$-(x-$\frac{3}{2}kπ$)]=cos(x-$\frac{3}{2}kπ$)
∴f(x)=$\left\{\begin{array}{l}{cos(x-\frac{3}{2}kπ),(\frac{3}{2}kπ-\frac{π}{2}≤x≤\frac{3}{2}kπ+\frac{π}{4})}\\{sin(x-\frac{3}{2}kπ),(\frac{3}{2}kπ+\frac{π}{4}≤x≤\frac{3}{2}kπ+π)}\end{array}\right.$
在[0,$\frac{3π}{2}$]上的单调递增区间:[$\frac{π}{4}$,$\frac{π}{2}$],[π,$\frac{3π}{2}$];
(3)由(2)可得函数f(x)在[-$\frac{π}{2}$,π]上的图象为:
①当0$≤a<\frac{\sqrt{2}}{2}$或1时,f(x)=a(a为常数)有2个解,其和为$\frac{π}{2}$
②当a=$\frac{\sqrt{2}}{2}$时,f(x)=a(a为常数)有3个解,其和为$\frac{3}{4}π$.
③当$\frac{\sqrt{2}}{2}<a<1$时,f(x)=a(a为常数)有4个解,其和为π
∴当x∈[-$\frac{π}{2}$,$\frac{3kπ}{2}$+π](k∈N)时,记关于x的方程f(x)=a(a为常数)所有解的和为S(k),
则S(k)=$\left\{\begin{array}{l}{\frac{π}{2}(3{k}^{2}+4k+1),(0≤a<\frac{\sqrt{2}}{2}或a=1)}\\{\frac{3π}{4}(3{k}^{2}+4k+1),a=\frac{\sqrt{2}}{2}}\\{π(3{k}^{2}+4k+1),\frac{\sqrt{2}}{2}<a<1}\end{array}\right.$.
点评 本题考查了三角函数的图象、性质,考查了三角恒等变形,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 三棱锥A-BCD中,E是BC的中点,且BD=8,CD=6,BC=10,AB=AD=4$\sqrt{2}$.
三棱锥A-BCD中,E是BC的中点,且BD=8,CD=6,BC=10,AB=AD=4$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com