
分析 (Ⅰ)令n=1,可得a1=1,结合{an}是公差为2的等差数列,可得{an}的通项公式,
(Ⅱ)将其代入已知条件anbn+1+bn+1=nbn来求{bn}的通项公式;
解答 解:(Ⅰ)∵anbn+1+bn+1=nbn.
当n=1时,a1b2+b2=b1.
∵b1=1,b2=$\frac{1}{2}$,
∴a1=1,
又∵{an}是公差为2的等差数列,
∴an=1+2(n-1)=2n-1,
(Ⅱ)∵anbn+1+bn+1=nbn,
∴(2n-1)bn+1+bn+1=nbn.
化简,得
2bn+1=bn,即$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{1}{2}$,
∴数列{bn}是以1为首项,以$\frac{1}{2}$为公比的等比数列,
∴bn=($\frac{1}{2}$)n-1
点评 本题考查的知识点是数列的递推式,数列的通项公式,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 28 | B. | 76 | C. | 123 | D. | 199 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
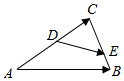 如图,D,E分别是△ABC的边AC,BC上的点,且$\overrightarrow{AD}$=$\overrightarrow{DC}$,$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{EC}$.若$\overrightarrow{DE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的值为$\frac{1}{2}$.
如图,D,E分别是△ABC的边AC,BC上的点,且$\overrightarrow{AD}$=$\overrightarrow{DC}$,$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{EC}$.若$\overrightarrow{DE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的值为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com