Question

18．已知如图是一个空间几何体的三视图．
（1）该空间几何体是如何构成的；
（2）求该几何体的表面积．

Answer 1

分析 （1）由三视图得到几何体是四棱柱与四棱锥的组合体；
（2）根据图中数据计算各面面积，求出表面积．

解答 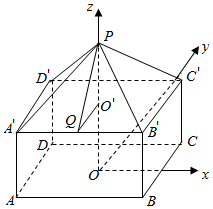解：（1）这个空间几何体的下半部分是一个底面边长为2正方形，高为1长方体…．（2分）
上半部分是一个底面边长为2正方形高为1四棱锥…．（4分）
（2）由题意可知，该几何体是由长方体ABCD-A'B'C'D'，P-A'B'C'D'

AB=AD=2，AA'=1，PO'=1，A'B'⊥PQ，
PQ=$\sqrt{PO{'}^{2}+O'{Q}^{2}}=\sqrt{2}$，
S=$\frac{1}{2}$（A'B'+B'C'+C'D'+D'A'）PQ+（A'B'+B'C'+C'D'+D'A'）AA'+AB•AD=4$\sqrt{2}$+12．

点评 本题考查了由几何体的三视图求几何体的表面积；关键是正确还原几何体．