
分析 (1)当a=-1,b=1时,f′(x)=(x2+3x+2)ex=(x+2)(x+1)ex,由此利用导数性质能求出f(x)的单调区间.
(2)①当b=a+1时,f(x)=(x2-ax+a+1)ex,求出导数,运用判别式大于0,解不等式即可得到所求范围;②问题等价于m>$\frac{f({x}_{2})}{{x}_{1}{e}^{{x}_{2}}}$=$\frac{{{x}_{2}}^{2}-a{x}_{2}+a+1}{{x}_{1}}$恒成立,即m>-x22+2x2+1恒成立,令t=a-2(t>2),由x2=$\frac{a-2+\sqrt{{a}^{2}-4a}}{2}$,令g(t)=$\frac{t+\sqrt{{t}^{2}-4}}{2}$,根据函数的单调性求出g(t)的最小值,从而求出m的范围.
解答 解:(1)当a=-1,b=1时,f(x)=(x2+x+1)ex,
f′(x)=(2x+1)ex+(x2+x+1)ex,
f′(x)=(x2+3x+2)ex=(x+2)(x+1)ex,
x∈(-∞,-2),f′(x)>0,f(x)是增函数,
x∈(-2,-1),f′(x)<0,f(x)是减函数,
x∈(-1,+∞),f′(x)>0,f(x)是增函数,
∴f(x)的单调增区间是(-∞,-2),(-1,+∞),f(x)的减区间是(-2,-1).
(2)①当b=a+1时,f(x)=(x2-ax+a+1)ex,
f′(x)=(2x-a)ex+(x2-ax+a+1)ex=[x2+(2-a)x+1)ex,
∵f′(x)=0有2根x1,x2,
∴△=(2-a)2-4>0,解得a>4或a<0,
则实数a的取值范围为(-∞,0)∪(4,+∞);
②a>0且mx1e${\;}^{{x}_{2}}$-f(x2)>0恒成立,
则a>4且x1+x2=a-2,x1x2=1,
∴x1>0,m>$\frac{f({x}_{2})}{{x}_{1}{e}^{{x}_{2}}}$=$\frac{{{x}_{2}}^{2}-a{x}_{2}+a+1}{{x}_{1}}$恒成立,
由于a=2+x1+x2,
即m>-x22+2x2+1恒成立,
令t=a-2(t>2),由x2=$\frac{a-2+\sqrt{{a}^{2}-4a}}{2}$,
令g(t)=$\frac{t+\sqrt{{t}^{2}-4}}{2}$,
t>2时,函数g(t)=$\frac{t+\sqrt{{t}^{2}-4}}{2}$递增,g(t)>g(2)=1,
∴x2>1,∴--x22+2x2+1<2,
故m的范围是[2,+∞).
点评 本题考查函数的单调性问题,考查导数的应用,解决与不等式有关的参数范围和证明问题,考查函数与方程思想、转化与化归思想,分类思想,考查运算能力,是一道综合题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{7}{32}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 28 | B. | 76 | C. | 123 | D. | 199 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | a3>b3 | C. | $\frac{1}{a}$$<\frac{1}{b}$ | D. | ac>bc |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
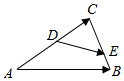 如图,D,E分别是△ABC的边AC,BC上的点,且$\overrightarrow{AD}$=$\overrightarrow{DC}$,$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{EC}$.若$\overrightarrow{DE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的值为$\frac{1}{2}$.
如图,D,E分别是△ABC的边AC,BC上的点,且$\overrightarrow{AD}$=$\overrightarrow{DC}$,$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{EC}$.若$\overrightarrow{DE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的值为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | -6 | C. | 2 | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com