
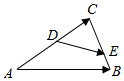
 ��ͼ��D��E�ֱ��ǡ�ABC�ı�AC��BC�ϵĵ㣬��$\overrightarrow{AD}$=$\overrightarrow{DC}$��$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{EC}$����$\overrightarrow{DE}$=��$\overrightarrow{AB}$+��$\overrightarrow{AC}$���ˣ��̡�R�������+�̵�ֵΪ$\frac{1}{2}$��
��ͼ��D��E�ֱ��ǡ�ABC�ı�AC��BC�ϵĵ㣬��$\overrightarrow{AD}$=$\overrightarrow{DC}$��$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{EC}$����$\overrightarrow{DE}$=��$\overrightarrow{AB}$+��$\overrightarrow{AC}$���ˣ��̡�R�������+�̵�ֵΪ$\frac{1}{2}$�� ���� $\overrightarrow{DE}$=$\overrightarrow{DC}+\overrightarrow{CE}$=$\frac{1}{2}\overrightarrow{AC}$+$\frac{2}{3}\overrightarrow{CB}$=$\frac{1}{2}\overrightarrow{AC}$+$\frac{2}{3}��\overrightarrow{AB}-\overrightarrow{AC}��$=$\frac{2}{3}\overrightarrow{AB}$-$\frac{1}{6}\overrightarrow{AC}$.$��=\frac{2}{3}$��$��=-\frac{1}{6}$��������æ�+�̣�
��� �⣺$\overrightarrow{DE}$=$\overrightarrow{DC}+\overrightarrow{CE}$=$\frac{1}{2}\overrightarrow{AC}$+$\frac{2}{3}\overrightarrow{CB}$=$\frac{1}{2}\overrightarrow{AC}$+$\frac{2}{3}��\overrightarrow{AB}-\overrightarrow{AC}��$=$\frac{2}{3}\overrightarrow{AB}$-$\frac{1}{6}\overrightarrow{AC}$��
��$��=\frac{2}{3}$��$��=-\frac{1}{6}$
���+��=$\frac{2}{3}-\frac{1}{6}=\frac{1}{2}$��
�ʴ�Ϊ��$\frac{1}{2}$
���� ���⿼�����������������㣬�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �������ԱȽϴ�С������Ҳ���ԱȽϴ�С | |
| B�� | ����ͬ���������ܱȽϴ�С����ͬ��Ŀ��ԱȽϴ�С | |
| C�� | �����Ĵ�С�뷽���й� | |
| D�� | ������ģ���ԱȽϴ�С |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com