
【题目】已知点A,B分别在射线CM,CN(不含端点C)上运动,∠MCN= ![]() ,在△ABC中,角A,B,C所对的边分别是a,b,c
,在△ABC中,角A,B,C所对的边分别是a,b,c 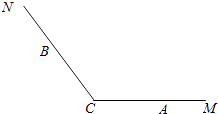
(1)若a,b,c依次成等差数列,且公差为2,求c的值:
(2)若c= ![]() ,∠ABC=θ,试用θ表示△ABC的周长,并求周长的最大值.
,∠ABC=θ,试用θ表示△ABC的周长,并求周长的最大值.
【答案】
(1)解:∵a,b,c依次成等差数列,且公差为2
∴a=c﹣4,b=c﹣2,
在△ABC中,∵ ![]() ,
,
由余弦定理可得cos∠MCN= ![]() =﹣
=﹣ ![]() ,
,
代值并整理可得c2﹣9c+14=0,解得c=2或c=7,
∵a=c﹣4>0,∴c>4,∴c=7
(2)解:由题意可得周长y=2sinθ+2sin( ![]() ﹣θ)+
﹣θ)+ ![]()
=2sin( ![]() +θ)+
+θ)+ ![]() ,
,
∴当 ![]() +θ=
+θ= ![]() 即θ=
即θ= ![]() 时,周长取最大值2+
时,周长取最大值2+ ![]()
【解析】(1)由题意可得a=c﹣4,b=c﹣2,由余弦定理cos∠MCN= ![]() =﹣
=﹣ ![]() 可得c的方程,解方程验证即可;(2)由题意可得周长y=2sinθ+2sin(
可得c的方程,解方程验证即可;(2)由题意可得周长y=2sinθ+2sin( ![]() ﹣θ)+
﹣θ)+ ![]() =2sin(
=2sin( ![]() +θ)+
+θ)+ ![]() ,由三角函数的最值可得.
,由三角函数的最值可得.
【考点精析】通过灵活运用余弦定理的定义,掌握余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此题.
即可以解答此题.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 过两点
过两点![]() ,
, ![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)直线![]() 过点
过点![]() 且与圆
且与圆![]() 有两个不同的交点
有两个不同的交点![]() ,
, ![]() ,若直线
,若直线![]() 的斜率
的斜率![]() 大于0,求
大于0,求![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,是否存在直线![]() 使得弦
使得弦![]() 的垂直平分线过点
的垂直平分线过点![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱台![]() 的上下底面分别是边长为2和4的正方形,
的上下底面分别是边长为2和4的正方形, ![]() = 4且
= 4且 ![]() ⊥底面
⊥底面![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
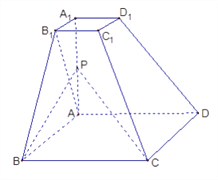
(Ⅰ)求证: ![]() 面
面 ![]() ;
;
(Ⅱ)在![]() 边上找一点
边上找一点![]() ,使
,使![]() ∥面
∥面![]() ,
,
并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明同学在寒假社会实践活动中,对白天平均气温与某家奶茶店的![]() 品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温
品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温![]() (
(![]() )与该奶茶店的
)与该奶茶店的![]() 品牌饮料销量
品牌饮料销量![]() (杯),得到如表数据:
(杯),得到如表数据:
日期 | 1月11号 | 1月12号 | 1月13号 | 1月14号 | 1月15号 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程式
的线性回归方程式![]() ;
;
(3)根据(2)所得的线性回归方程,若天气预报1月16号的白天平均气温为![]() ,请预测该奶茶店这种饮料的销量.
,请预测该奶茶店这种饮料的销量.
(参考公式: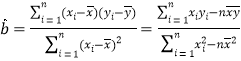 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
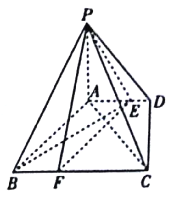
(Ⅰ)已知点![]() 在
在![]() 上,且
上,且![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的余弦值为多少时,直线
的余弦值为多少时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)一块长为![]() 、宽为
、宽为![]() 的长方形铁片,铁片的四角截去四个边长均为
的长方形铁片,铁片的四角截去四个边长均为![]() 的小正方形,然后做成一个无盖方盒.
的小正方形,然后做成一个无盖方盒.
(Ⅰ)试把方盒的容积V表示为![]() 的函数;
的函数;
(Ⅱ)试求方盒容积V的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.
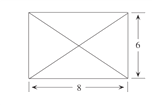
(1)求该几何体的体积![]() ;
;
(2)求该几何体的表面积![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com