【题目】已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形．
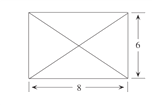
(1)求该几何体的体积
;
(2)求该几何体的表面积
.
口算题卡北京妇女儿童出版社系列答案科目：高中数学 来源： 题型：
【题目】已知点A，B分别在射线CM，CN（不含端点C）上运动，∠MCN= 
，在△ABC中，角A，B，C所对的边分别是a，b，c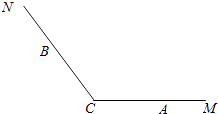 
（1）若a，b，c依次成等差数列，且公差为2，求c的值：
（2）若c= 
，∠ABC=θ，试用θ表示△ABC的周长，并求周长的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
、
分别是椭圆
的左顶点、右焦点，点
为椭圆
上一动点，当
轴时， 
.
（1）求椭圆
的离心率；
（2）若椭圆
存在点
，使得四边形
是平行四边形（点
在第一象限），求直线
与
的斜率之积；
（3）记圆
为椭圆
的“关联圆”. 若
，过点
作椭圆
的“关联圆”的两条切线，切点为
、
，直线
的横、纵截距分别为
、
，求证： 
为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
： 
（
），设
为圆
与
轴负半轴的交点，过点
作圆
的弦
，并使弦
的中点恰好落在
轴上．
（Ⅰ）求点
的轨迹
的方程；
（Ⅱ）延长
交曲线
于点
，曲线
在点
处的切线与直线
交于点
，试判断以点
为圆心，线段
长为半径的圆与直线
的位置关系，并证明你的结论．
查看答案和解析>>
科目：高中数学 来源： 题型：
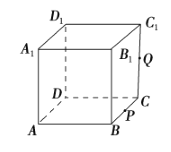
【题目】如图，正方体
的棱长为 1， 
为
的中点， 
为线段
上的动点，过点A、P、Q的平面截该正方体所得的截面记为
.则下列命题正确的是__________(写出所有正确命题的编号)．
①当
时， 
为四边形；②当
时， 
为等腰梯形；③当
时， 
为六边形；④当
时， 
的面积为
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高三年级一次数学考试后，为了解学生的数学学习情况，随机抽取
名学生的数学成绩，制成表所示的频率分布表.
组号 | 分组 | 频数 | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
合计 |
|
| |
（1）求
、
、
的值；
（2）若从第三、四、五组中用分层抽样方法抽取
名学生，并在这
名学生中随机抽取
名学生与张老师面谈，求第三组中至少有
名学生与张老师面谈的概率
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图为一简单组合体，其底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD=AD=2EC=2．
（1）请画出该几何体的三视图；
（2）求四棱锥B﹣CEPD的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线l过点A（﹣3，4）
（1）若l与直线y=﹣2x+5平行，求其一般式方程；
（2）若l与直线y=﹣2x+5垂直，求其一般式方程；
（3）若l与两个坐标轴的截距之和等于12，求其一般式方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
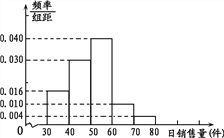
【题目】某超市计划销售某种产品，先试销该产品
天，对这
天日销售量进行统计，得到频率分布直方图如图．
（Ⅰ）若已知销售量低于50的天数为23，求
；
（Ⅱ）厂家对该超市销售这种产品的日返利方案为：每天固定返利45元，另外每销售一件产品，返利3元；频率估计为概率．依此方案，估计日返利额的平均值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
