
【题目】已知直线l过点A(﹣3,4)
(1)若l与直线y=﹣2x+5平行,求其一般式方程;
(2)若l与直线y=﹣2x+5垂直,求其一般式方程;
(3)若l与两个坐标轴的截距之和等于12,求其一般式方程.
【答案】解:(1)设直线l的方程为:y=﹣2x+m,把点A(﹣3,4)代入可得:4=﹣2×(﹣3)+m,解得m=﹣2,可得直线l的方程为:2x+y+2=0.
(2)设直线l的方程为:y=![]() x+n,把点A(﹣3,4)代入可得:4=
x+n,把点A(﹣3,4)代入可得:4=![]() ×(﹣3)+n,解得n=
×(﹣3)+n,解得n=![]() ,可得直线l的方程为:x﹣2y+11=0.
,可得直线l的方程为:x﹣2y+11=0.
(3)设直线l的方程为:![]() =1,把点A(﹣3,4)代入可得
=1,把点A(﹣3,4)代入可得![]() +
+![]() =1,与a+b=12联立解得:
=1,与a+b=12联立解得:![]() ,或
,或![]() .
.
可得直线l的方程为:x+3y﹣9=0或4x﹣y+16=0.
【解析】(1)设直线l的方程为:y=﹣2x+m,把点A(﹣3,4)代入解得m即可得出方程.
(2)设直线l的方程为:y=![]() x+n,把点A(﹣3,4)代入解得n即可得出方程.
x+n,把点A(﹣3,4)代入解得n即可得出方程.
(3)设直线l的方程为:![]() =1,把点A(﹣3,4)代入可得
=1,把点A(﹣3,4)代入可得![]() +
+![]() =1,与a+b=12联立解得a,b即可得出方程.
=1,与a+b=12联立解得a,b即可得出方程.


科目:高中数学 来源: 题型:
【题目】(本题满分12分)一块长为![]() 、宽为
、宽为![]() 的长方形铁片,铁片的四角截去四个边长均为
的长方形铁片,铁片的四角截去四个边长均为![]() 的小正方形,然后做成一个无盖方盒.
的小正方形,然后做成一个无盖方盒.
(Ⅰ)试把方盒的容积V表示为![]() 的函数;
的函数;
(Ⅱ)试求方盒容积V的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.
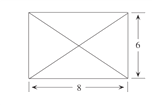
(1)求该几何体的体积![]() ;
;
(2)求该几何体的表面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2mx+m2+4m﹣2.
(1)若函数f(x)在区间[0,1]上是单调递减函数,求实数m的取值范围;
(2)若函数f(x)在区间[0,1]上有最小值﹣3,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,直线
为坐标原点,直线![]() 的方程为
的方程为![]() ,点
,点![]() 是抛物线
是抛物线![]() 上到直线
上到直线![]() 距离最小的点,点
距离最小的点,点![]() 是抛物线上异于点
是抛物线上异于点![]() 的点,直线
的点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,过点
,过点![]() 与
与![]() 轴平行的直线与抛物线
轴平行的直线与抛物线![]() 交于点
交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求证:直线![]() 恒过定点
恒过定点![]() ;
;
(3)在(2)的条件下过![]() 向
向![]() 轴做垂线,垂足为
轴做垂线,垂足为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨;生产乙种棉纱1吨需耗一级籽棉1吨,二级籽棉2吨.每1吨甲种棉纱的利润为900元,每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中,要求消耗一级籽棉不超过250吨,二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨,能使利润总额最大?并求出利润总额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正△ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是( )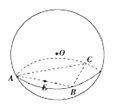
A.![]()
B.2π
C.![]()
D.3π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).
(1)写出楼房平均综合费用y关于建造层数x的函数关系式;
(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com