
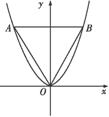
如图,等边三角形OAB的边长为8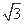 ,且其三个顶点均在抛物线E:x2=2py
,且其三个顶点均在抛物线E:x2=2py
(p>0)上.
(1)求抛物线E的方程;
(2)设动直线l与抛物线E相切于点P,与直线y=-1相交于点Q,证明以PQ为直径的圆恒过y轴上某定点.
(1)解:依题意,|OB|=8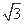 ,∠BOy=30°.
,∠BOy=30°.
设B(x,y),则x=|OB|sin 30°=4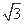 ,
,
y=|OB|cos 30°=12.
因为点B(4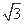 ,12)在x2=2py上,
,12)在x2=2py上,
所以(4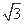 )2=2p×12,解得p=2.
)2=2p×12,解得p=2.
故抛物线E的方程为x2=4y.
(2)证明:由(1)知y= x2,y′=
x2,y′=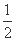 x.
x.
设P(x0,y0),则x0≠0,y0= ,且l的方程为
,且l的方程为
y-y0=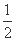 x0(x-x0),即y=
x0(x-x0),即y=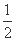 x0x-
x0x- .
.
由 得
得
所以Q为 .
.
设M(0,y1),令 ·
· =0对满足y0=
=0对满足y0= (x0≠0)的x0,y0恒成立.
(x0≠0)的x0,y0恒成立.
由于 =(x0,y0-y1),
=(x0,y0-y1),  =
= ,
,
由 ·
· =0,
=0,
得 -y0-y0y1+y1+
-y0-y0y1+y1+ =0,
=0,
即( +y1-2)+(1-y1)y0=0.(*)
+y1-2)+(1-y1)y0=0.(*)
由于(*)式对满足y0= (x0≠0)的y0恒成立,
(x0≠0)的y0恒成立,
所以
解得y1=1.
故以PQ为直径的圆恒过y轴上的定点M(0,1).


科目:高中数学 来源: 题型:
设α∈{-1,1,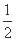 ,3},则使函数y=xα的定义域为R且为奇函数的所有α值为( )
,3},则使函数y=xα的定义域为R且为奇函数的所有α值为( )
(A)1,3 (B)-1,1
(C)-1,3 (D)-1,1,3
解
查看答案和解析>>
科目:高中数学 来源: 题型:
设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( )
(A)(0,2) (B)[0,2]
(C)(2,+∞) (D)[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009年大纲全国卷Ⅱ,文11)已知直线y=k(x+2)(k>0)与抛物线C:y2=8x相交于A、B两点,F为C的焦点,若|FA|=2|FB|,则k等于( )
(A)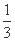 (B)
(B)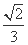 (C)
(C)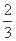 (D)
(D)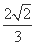
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线y2=2px(p>0)的焦点F与双曲线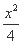 -
- =1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|=
=1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|=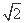 |AF|,则A点的横坐标为( )
|AF|,则A点的横坐标为( )
(A)2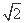 (B)3 (C)2
(B)3 (C)2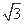 (D)4
(D)4
查看答案和解析>>
科目:高中数学 来源: 题型:
设动点P(x,y)(x≥0)到定点F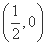 的距离比到y轴的距离大
的距离比到y轴的距离大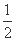 .记点P的轨迹为曲线C.
.记点P的轨迹为曲线C.
(1)求点P的轨迹方程;
(2)设圆M过A(1,0),且圆心M在P的轨迹上,BD是圆M在y轴上截得的弦,当M运动时弦长BD是否为定值?说明理由;
(3)过F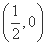 作互相垂直的两直线交曲线C于G、H、R、S,求四边形GRHS面积的最小值.
作互相垂直的两直线交曲线C于G、H、R、S,求四边形GRHS面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
设a,b,c,d∈(0,+∞),若a+d=b+c且|a-d|<|b-c|,则有( )
(A)ad=bc (B)ad<bc
(C)ad>bc (D)ad≤bc
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com