
已知某几何体的直观图(图1)与它的三视图(图2),其中俯视图为正三角形,主视图及左视图是矩形.
(1)求出该几何体的体积;
(2) 是棱
是棱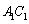 上的一点,若使直线
上的一点,若使直线 ,试确定点
,试确定点 的位置,并证明你的结论;
的位置,并证明你的结论;
(3)在(2)成立的条件下,求证:平面 .
.
 |
解:由三视图可知该几何体为正三棱柱,底面是高为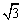 的正三角形,三棱柱的高
的正三角形,三棱柱的高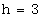 ,……………………………………………… 2分
,……………………………………………… 2分
(1)底面是高为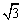 的正三角形,易知底面边长为2,
的正三角形,易知底面边长为2,
所以底面面积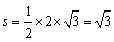 ,
,
所求体积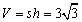 . …………………… 4分
. …………………… 4分
(2)连接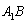 ,且
,且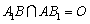 ,因为正三棱柱侧面是矩形,所以点
,因为正三棱柱侧面是矩形,所以点 是
是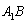 的中点, ………… 5分
的中点, ………… 5分
(方法一)若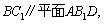
连接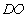 ,
,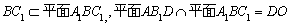 ,
,
所以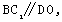 所以
所以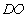 是
是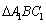 的中位线,所以D为
的中位线,所以D为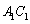 的中点.
的中点.
即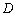 为
为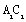 的中点时,
的中点时, . ………………………………… 8分
. ………………………………… 8分
(方法二)若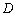 为棱
为棱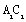 的中点.
的中点.
连接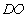 ,所以
,所以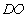 是
是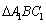 的中位线,
的中位线,
所以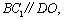 又
又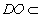
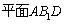 ,
,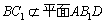 ,所以
,所以 .
.
即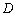 为
为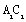 的中点时,
的中点时, . ………………………………… 8分
. ………………………………… 8分
(方法三)在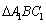 中,过
中,过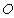 作
作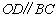 1,交
1,交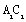 与D,所以
与D,所以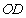 为
为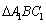 的中位线,所以
的中位线,所以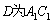 的中点,又
的中点,又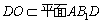 ,
,
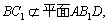 所以
所以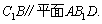
即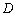 为
为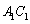 的中点时,
的中点时, . ………………………………… 8分
. ………………………………… 8分
(3)(方法一)在正三棱柱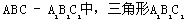 为正三角形,所以
为正三角形,所以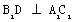 ,
,
又由三棱柱性质知 且
且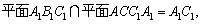
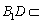 平面
平面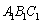 ,所以
,所以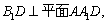 ……………………………… 10分
……………………………… 10分
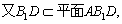 所以
所以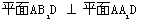 . ………………………… 12分
. ………………………… 12分
(方法二)在正三棱柱ABC-A1B1C1中,三角形A1B1C1为正三角形,所以B1D⊥A1C1,又因为AA1⊥平面A1B1C1,所以AA1⊥B1D. AA1 A1C1=A1,AA1
A1C1=A1,AA1 平面AA1D,A1 C1
平面AA1D,A1 C1 平面AA1D,所以B1D⊥平面AA1D,………………………………………… 10分
平面AA1D,所以B1D⊥平面AA1D,………………………………………… 10分
又B1D 平面AB1D,所以平面AB1D⊥平面AA1D. ………………………… 12分
平面AB1D,所以平面AB1D⊥平面AA1D. ………………………… 12分


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
将下列说法中,正确说法序号写在后面的横线上 .
①至少有一个整数x,能使5x-1是整数;
②对于 ;
;
③ 是
是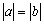 的充要条件;
的充要条件;
④若命题 为周期函数;
为周期函数; 为偶函数,则
为偶函数,则 为真命题.
为真命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在底面ABCD为平行四边形的四棱柱ABCD-A1B1C1D1
中,M 是AC与BD的交点,若 ,
,
则下列向量中与 相等的向量是( )
相等的向量是( )
A. B.
B. 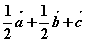
C.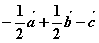 D.
D.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com