用数学归纳法证明：12＋32＋52＋…＋(2n－1)2＝
n(4n2－1)．
证明 (1)当n＝1时，左边＝12＝1，
右边＝×1×(4－1)＝1，等式成立．
(2)假设当n＝k(k∈N*)时等式成立，即12＋32＋52＋…＋(2k－1)2＝k(4k2－1)．
则当n＝k＋1时，12＋32＋52＋…＋(2k－1)2＋(2k＋1)2
＝k(4k2－1)＋(2k＋1)2＝k(4k2－1)＋4k2＋4k＋1
＝k[4(k＋1)2－1]－k·4(2k＋1)＋4k2＋4k＋1
＝k[4(k＋1)2－1]＋(12k2＋12k＋3－8k2－4k)
＝k[4(k＋1)2－1]＋[4(k＋1)2－1]
＝(k＋1)[4(k＋1)2－1]．
即当n＝k＋1时等式也成立．
由(1)，(2)可知，对一切n∈N*，等式都成立．
暑假作业暑假快乐练西安出版社系列答案科目：高中数学 来源： 题型：
设Sn表示数列{an}的前n项和．
(1)若{an}为等差数列，推导Sn的计算公式；
(2)若a1＝1，q≠0，且对所有正整数n，有Sn＝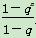
，判断{an}是否为等比数列，并证明你的结论．
查看答案和解析>>
科目：高中数学 来源： 题型：
观察下列算式：
13＝1，
23＝3＋5，
33＝7＋9＋11，
43＝13＋15＋17＋19，
……
若某数m3按上述规律展开后，发现等式右边含有“2 013”这个数，则m＝________.
查看答案和解析>>
科目：高中数学 来源： 题型：
设函数f(x)＝ln(1＋x)，g(x)＝xf′(x)，x≥0，其中f′(x)是f(x)的导函数．
(1)令g1(x)＝g(x)，gn＋1(x)＝g(gn(x))，n∈N*，求gn(x)的表达式；
(2)若f(x)≥ag(x)恒成立，求实数a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
图象上存在不同的三点到原点的距离构成等比数列，则以下不可能成为公比的数是( )
B.
D.
的解集是________．