
设函数f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的导函数.
(1)令g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N*,求gn(x)的表达式;
(2)若f(x)≥ag(x)恒成立,求实数a的取值范围.
解 由题设得,g(x)=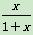 (x≥0).
(x≥0).
(1)由已知得,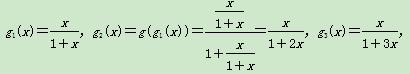 …,可得gn(x)=
…,可得gn(x)=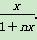 .
.
下面用数学归纳法证明.
①当n=1时,g1(x)=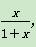 ,结论成立.
,结论成立.
②假设n=k时结论成立,
即gk(x)=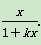 .
.
那么,当n=k+1时,gk+1(x)=g(gk(x))=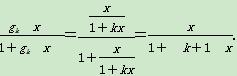 即结论成立.
即结论成立.
由①②可知,结论对n∈N*成立.
(2)已知f(x)≥ag(x)恒成立,
即ln(1+x)≥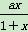 恒成立.
恒成立.
设φ(x)=ln(1+x)-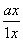 (x≥0),
(x≥0),
即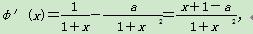 ,
,
当a≤1时,φ′(x)≥0(仅当x=0,a=1时等号成立),
∴φ(x)在[0,+∞)上单调递增,又φ(0)=0,
∴φ(x)≥0在[0,+∞)上恒成立,
∴a≤1时,ln(1+x)≥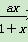 恒成立(仅当x=0时等号成立).
恒成立(仅当x=0时等号成立).
当a>1时,对x∈(0,a-1]有φ′(x)<0,
∴φ(x)在(0,a-1]上单调递减,
∴φ(a-1)<φ(0)=0.
即a>1时,存在x>0,使φ(x)<0,故知ln(1+x)≥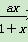 不恒成立,
不恒成立,
综上可知,a的取值范围是(-∞,1].


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
据科学计算,运载“神舟”的“长征”二号系列火箭在点火后第一秒钟通过的路程为2 km,以后每秒钟通过的路程增加2 km,在到达离地面240 km的高度时,火箭与飞船分离,则这一过程需要的时间是( )
A.10秒钟 B.13秒钟
C.15秒钟 D.20秒钟
查看答案和解析>>
科目:高中数学 来源: 题型:
用数学归纳法证明等式1+3+5+…+(2n+1)=(n+1)2(n∈N*)的过程中,第二步假设n=k时等式成立,则当n=k+1时应得到( )
A.1+3+5+…+(2k+1)=k2
B.1+3+5+…+(2k+3)=(k+2)2
C.1+3+5+…+(2k+1)=(k+2)2
D.1+3+5+…+(2k+3)=(k+3)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com