练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用数学归纳法证明等式1＋3＋5＋…＋(2n＋1)＝(n＋1)2(n∈N*)的过程中，第二步假设n＝k时等式成立，则当n＝k＋1时应得到(　　)

    A．1＋3＋5＋…＋(2k＋1)＝k2

    B．1＋3＋5＋…＋(2k＋3)＝(k＋2)2

    C．1＋3＋5＋…＋(2k＋1)＝(k＋2)2

    D．1＋3＋5＋…＋(2k＋3)＝(k＋3)2


    B


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设等比数列{an}的前n项和为Sn.若S2＝3，S4＝15，则S6＝(　　)

    A．31                                   B．32

    C．63                                   D．64

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若P＝(a≥0)，则P，Q的大小关系(　　)

    A．P>Q                                  B．P＝Q

    C．P<Q                                  D．由a取值决定

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于数25，规定第1次操作为23＋53＝133，第2次操作为13＋33＋33＝55，如此反复操作，则第2 011次操作后得到的数是(　　)

    A．25                                   B．250

    C．55                                   D．133

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    观察下列算式：

    13＝1，

    23＝3＋5，

    33＝7＋9＋11，

    43＝13＋15＋17＋19，

    ……

    若某数m3按上述规律展开后，发现等式右边含有“2 013”这个数，则m＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若f(n)＝12＋22＋32＋…＋(2n)2，则f(k＋1)与f(k)的递推关系是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝ln(1＋x)，g(x)＝xf′(x)，x≥0，其中f′(x)是f(x)的导函数．

    (1)令g1(x)＝g(x)，gn＋1(x)＝g(gn(x))，n∈N*，求gn(x)的表达式；

    (2)若f(x)≥ag(x)恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A＝{x∈R||lg|x||≤1}，B＝{x∈Z|x2－2x－8<0}，则A∩B＝(　　)

    A．(－2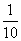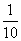，－)∪(，4)               B．(－2,0)∪(0,4)

    C．{－1,1,2,3}                          D．{－1,0,1,2,3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若正数a，b满足＋＝1，则的最小值为(　　)

    A．1                                    B．6

    C．9                                    D．16

    查看答案和解析>>

    同步练习册答案