
对于数25,规定第1次操作为23+53=133,第2次操作为13+33+33=55,如此反复操作,则第2 011次操作后得到的数是( )
A.25 B.250
C.55 D.133
科目:高中数学 来源: 题型:
已知函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列 (n∈N*)的前n项和为Sn,则S2 012的值为( )
(n∈N*)的前n项和为Sn,则S2 012的值为( )
A.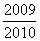 B.
B.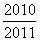
C.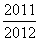 D.
D.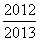
查看答案和解析>>
科目:高中数学 来源: 题型:
观察下表:
1,
2,3,
4,5,6,7,
8,9,10,11,12,13,14,15,
…,
问:(1)此表第n行的最后一个数是多少?
(2)此表第n行的各个数之和是多少?
(3)2 013是第几行的第几个数?
查看答案和解析>>
科目:高中数学 来源: 题型:
用数学归纳法证明等式1+3+5+…+(2n+1)=(n+1)2(n∈N*)的过程中,第二步假设n=k时等式成立,则当n=k+1时应得到( )
A.1+3+5+…+(2k+1)=k2
B.1+3+5+…+(2k+3)=(k+2)2
C.1+3+5+…+(2k+1)=(k+2)2
D.1+3+5+…+(2k+3)=(k+3)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com